
This article and others are included in the 18 chapters of
a 164 page paperback compilation of articles by JMW
$19.95
US list at Amazon
Click
here for Amazon.com
Nucleotopes
and The Nuclei of the Elemental Isotopes
By Joel M Williams ©2014

|
This article and others are included in the 18 chapters of a 164 page paperback compilation of articles by JMW $19.95
US list at Amazon
|
Royal Society "Open Science" has deemed this paper unfit for inquiring eyes
based on this lone (quoted in its entirety) review: "The proposed model is in conflict with more than half a century of basic nuclear and atomic data (magic numbers, charge measurements of ions, nuclear mass measurements, fragmentation, to name a few) and all data supporting the Cabibbo–Kobayashi–Maskawa matrix of the standard model of particle physics."
"Charge measurements of ions" is not even discussed and the
"nuclear mass measurements" used are those in the literature!
Asserting that data supporting one model automatically excludes all other models
is faulty reasoning.
Adherents of the standard model would not want any new and significantly different model in the literature. In an "open science" world, ALL conceivable models would be aired!
Introduction
 "The
nucleus of an atom consists of protons and neutrons (two types of baryons) bound
by the nuclear force (also known as the residual strong force). These baryons
are further composed of subatomic fundamental particles known as quarks1 bound by
the strong interaction. Which chemical element an atom represents is determined
by the number of protons in the nucleus. Each proton carries a single positive
charge, and the total electrical charge of the nucleus is spread fairly
uniformly throughout its body."2
This view is little different than it was a century ago, except for the quarks.
"The
nucleus of an atom consists of protons and neutrons (two types of baryons) bound
by the nuclear force (also known as the residual strong force). These baryons
are further composed of subatomic fundamental particles known as quarks1 bound by
the strong interaction. Which chemical element an atom represents is determined
by the number of protons in the nucleus. Each proton carries a single positive
charge, and the total electrical charge of the nucleus is spread fairly
uniformly throughout its body."2
This view is little different than it was a century ago, except for the quarks.
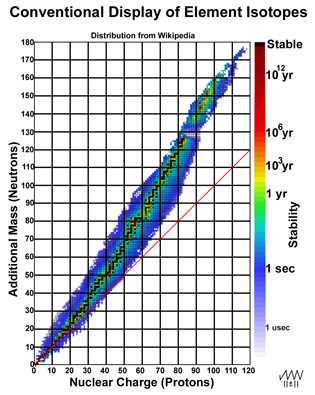
"While protons define the entire charge of a nucleus and, hence, its chemical identity, neutrons are electrically neutral, but contribute to the mass of a nucleus to the same extent. Neutrons explain the phenomenon of isotopes – varieties of a chemical element which differ in atomic mass."2 The nucleus has minor influence on an element's chemistry beyond its charge and the orbitals of the electrons. Isotopes relate to chemistry; the character of the nuclei is a separate issue. In other words, the nuclei of an element's isotopes may have little in common with one another! Figure 1 (on the right) provides a typical display of the elements (nuclear charge/proton number/atomic number) with varying additional mass (neutrons) with each isotope color-coded3 to indicate its individual stability.
Figure 1. Conventional Plot of Elemental Isotopes
Plotting the distribution of the elemental isotopes as a function of their masses gives a decidedly different perspective of how the nuclei of the isotopes relate to one another. In Figure 2, the data in Figure 1 is tipped 45-degrees so that nuclear mass is evenly spaced along the x-axis. The y-axis grid is set 2 units/line with the 20-unit line passing through mercury (at #80, mass = 200) for reasons that will be clear later.
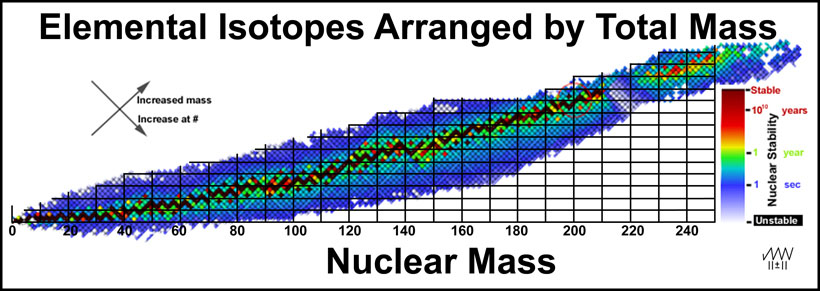
Figure 2. Elemental Isotopes Arranged by Total Mass
A number of general trends can be seen.
Before preceding to an explanation about the relationship of the nuclei of the different elements that have the same total mass, it is useful to explore the elements in the lowest mass region. The nuclei of the first eleven elements are illustrated in Figure 3. Beta-particle decays give vertical changes in elements without changing the nuclear mass: β- downward (increased atomic number) and β+ upward (decreased atomic number). Vertical changes should involve minor changes in the nucleus other than the beta-particle changes.
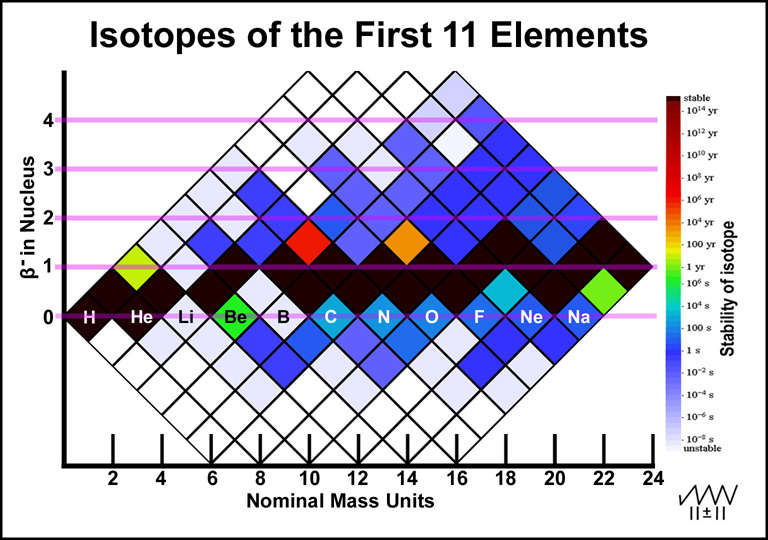
Figure 3. Isotopes of the First Eleven Elements
The first few elements do not have many ways for their nuclei to be assembled and therefore have few stable nuclei. Below are a few observations. Decay data is from Wikipedia.5
The Nucleotope Model of the Nucleus
 Without
belaboring the issue, suffice it to say that the conversion of a neutron to a
proton (down-quark converted to an up-quark) with the release of a β-
particle and a neutrino defies logic6
when up
and down quarks are considered basic, non-compounded, nuclear components.
Similarly, the conversion of a proton to a neutron (up-quark converted to a
down-quark) in the nucleus with the release of a
β+ particle also defies logic for the same reason. While
Feynman diagrams7 may describe such conversions, these quark conversions are,
nonetheless, still illogical. A more logical model would
have the β- and β+
particles derived from entities separate from the quarks which should remain
unaltered.
Without
belaboring the issue, suffice it to say that the conversion of a neutron to a
proton (down-quark converted to an up-quark) with the release of a β-
particle and a neutrino defies logic6
when up
and down quarks are considered basic, non-compounded, nuclear components.
Similarly, the conversion of a proton to a neutron (up-quark converted to a
down-quark) in the nucleus with the release of a
β+ particle also defies logic for the same reason. While
Feynman diagrams7 may describe such conversions, these quark conversions are,
nonetheless, still illogical. A more logical model would
have the β- and β+
particles derived from entities separate from the quarks which should remain
unaltered.
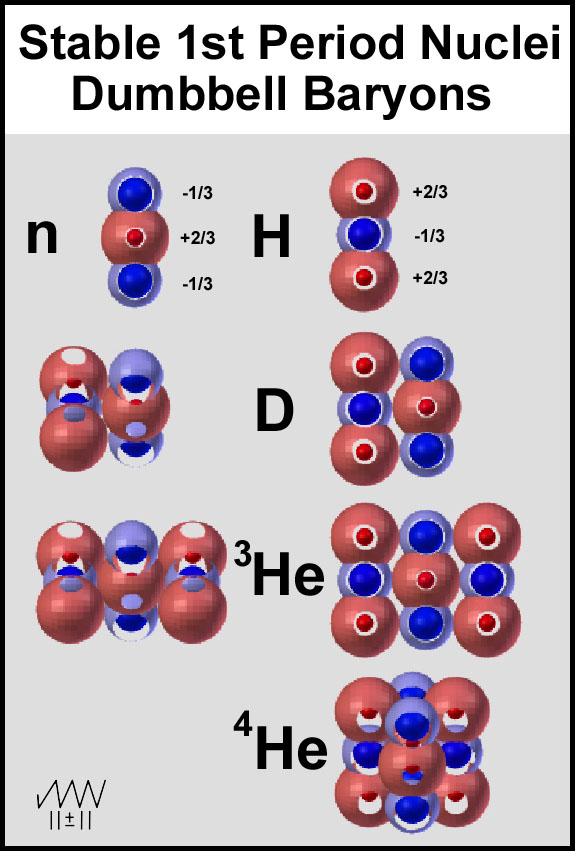
Dumbbell models of the baryons (proton and neutron) provide the essence of the
two observed quarks. While some would decry these dumbbells as too simplistic,
they do indicate strong, multiple, electrostatic interactions between the two
types of baryons. These features are presented in Figure 4. That the nucleus of
each element in Figure 4 is stable attests to the stability of the baryons.
Equal or near equal numbers of the two baryon types provide maximum
electrostatic interactions. It is logical that as the total number of baryons
increases that the baryons do so in pairs to maintain their template
interactions. This was the rationale for putting a "20" line in Figure
2 through the 200 mass isotope of Hg-80. The Hg-80/200 nucleus would be composed
of equal numbers of protons and neutrons (100 each) and
20 β- that set the outward charge of the nucleus to
positive 80.
Figure 4. Dumbbell Baryons of the First Period Elements
The y-axis of Figure 2 is now expanded in Figure 5 to show the effect of the included β- particles on the isotope stabilities more clearly. A periodic table8 is included for easy referencing to the elements.

Figure 5. Nucleotopes of the Elements
Isotopes of an element "step" with alternating "neutral baryonic pairs": (a neutron) and (a proton with a separate β- particle). Element to element changes of single mass units also "step", but do so with alternating "positive baryonic pairs": (a neutron minus a separate β- particle) and (a proton). Vertical changes from one element to another occur without a mass change, but with a β- particle release or addition. Horizontal changes from one element to another occur with a proton-neutron pair. Nuclear stability is related to the arrangement of the proton and neutron baryons with the added complication of accommodating the included β- particles. Some elements, e.g., Sn-50, have many possible stable nucleotopes and thus many stable isotopes. Promethium-61, on the other hand, has NO stable nucleotope arrangements and, thus, no stable isotopes.
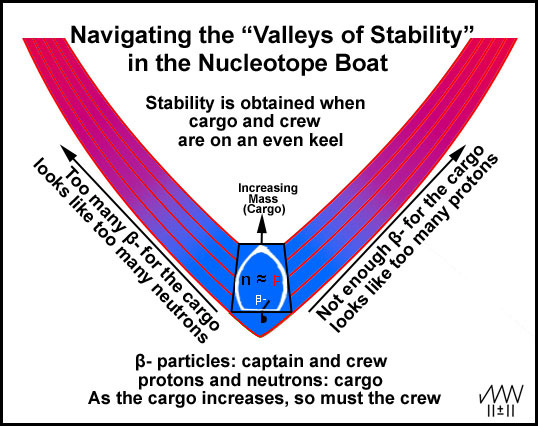 Why
is there a relatively narrow "stability zone" or "Valleys of
Stability"? Because the protons and neutrons need to be equal or not more
than one or two in either direction! The zone's location shifts from the
straight-and-narrow to accommodate the included β-
particles. It is the β- particles
that keep the nuclei on an even keel as the mass increases through the
"Valleys of Stability" (Figure 6). As the cargo (mass) increases, more
crew (β- particles) is
needed. Sometimes the nuclear boat must navigate through some rocky stretches
where the crew can find no stable arrangements.
Why
is there a relatively narrow "stability zone" or "Valleys of
Stability"? Because the protons and neutrons need to be equal or not more
than one or two in either direction! The zone's location shifts from the
straight-and-narrow to accommodate the included β-
particles. It is the β- particles
that keep the nuclei on an even keel as the mass increases through the
"Valleys of Stability" (Figure 6). As the cargo (mass) increases, more
crew (β- particles) is
needed. Sometimes the nuclear boat must navigate through some rocky stretches
where the crew can find no stable arrangements.
Figure 6. Navigating the "Valleys of Elemental Stability"
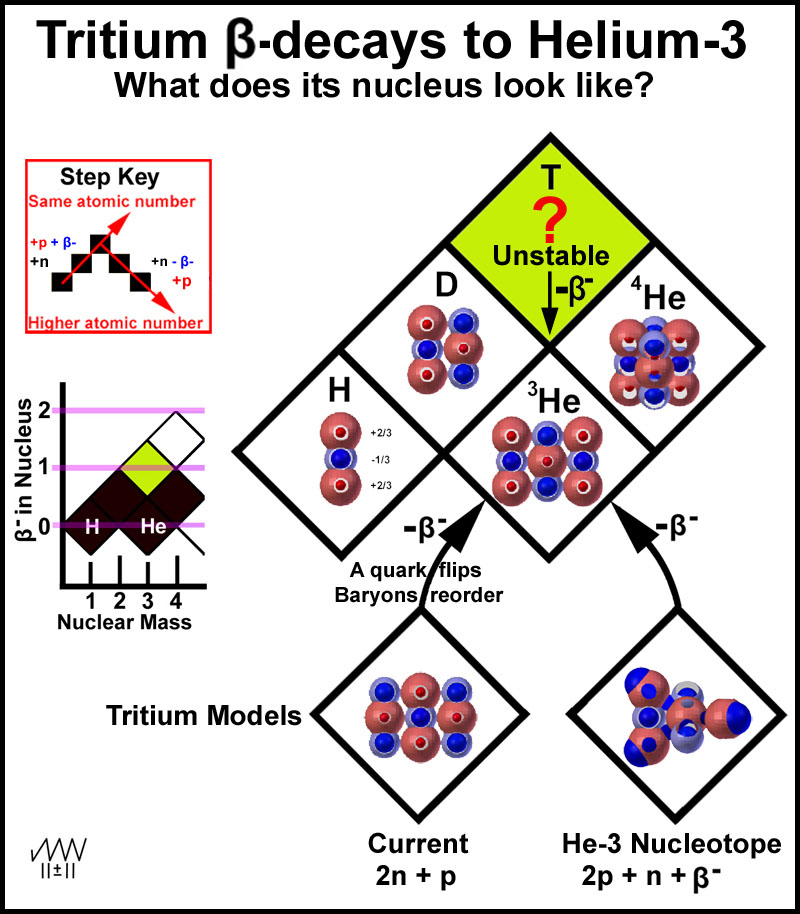 The
hydrogen-helium isotopes provide a simple contrast between the nucleotope model
and the current model with its over/under-loading of the nuclei with neutrons to
produce the elemental isotopes. Dumbbell models of the stable nuclei of the +1
and +2 nuclei have been placed in the diamonds of Figure 7. The question is what
model to put in the tritium diamond.
The
hydrogen-helium isotopes provide a simple contrast between the nucleotope model
and the current model with its over/under-loading of the nuclei with neutrons to
produce the elemental isotopes. Dumbbell models of the stable nuclei of the +1
and +2 nuclei have been placed in the diamonds of Figure 7. The question is what
model to put in the tritium diamond.
According to the step key of Figure 5, the tritium image should be the deuterium nucleus plus a proton plus a β- particle which is just the He-3 nucleus plus a β- particle! This, of course, is not the current model. The current and nucleotope dumbbell baryon models are shown at the bottom of Figure 7 for comparison. Both must liberate a β- particle as this is what tritium does to yield helium-3. The current model requires that a down quark be converted to an up quark with the β- particle being released in the process and that the baryons then reorder to produce maximum electrostatic interactions. Since most of the stable isotopes of the periodic table have many more neutrons than protons according to the current model, it is not clear why this model of tritium would have a propensity to decay at all.
Figure 7. Modeling the Isotopes of the First Two Elements

In contrast, the He-3 nucleotope tritium nucleus simply releases an included β- particle to yield the helium-3 nucleus. How is this β- particle incorporated in the tritium He-3 nucleus? It simply orbits, as indicated by the four blue orbital extremes in Figure 8, around the 5 +2/3 quarks in a manner similar to the tetrahedral movement of an external, nucleus-orbiting electron, ala the MCAS electron model9. What is the driving force for the decay of this nucleotope? The answer is the center neutron. This baryon has no single low energy position to provide ultimate stability. While the β- particle moves in its orbital path, the neutron oscillates in its plane. At some point, the down quarks of the neutron (light blue spheres) will be positioned just right to force the β- particle, as it move towards it outer limits, beyond its normal extreme and out of the nucleus. T-3 now decays to He-3 with nothing more than the β- particle and subsequent binding energy being released.
Figure 8. Tritium Nucleus - He-3 Nucleotope
Analyzing the Binding Energy of Nuclei
What is binding energy, but mass that is no longer there and has become energy somewhere else? Binding energy is calculated by the following equation where the mass of the nucleus is independent of its constituents:
Binding Energy = ∑(mass of the unbound nuclear components) - the mass of the nucleus
Ebinding = mass lost when the baryons shed some neutral matter to cozy up for more optimal electrostatic
______________ (pos-neg attraction and pos-pos/neg-neg repulsion) interactions
Binding energy per nuclear component using published data10 has been calculated for a number of elements and plotted11 in Figure 9.
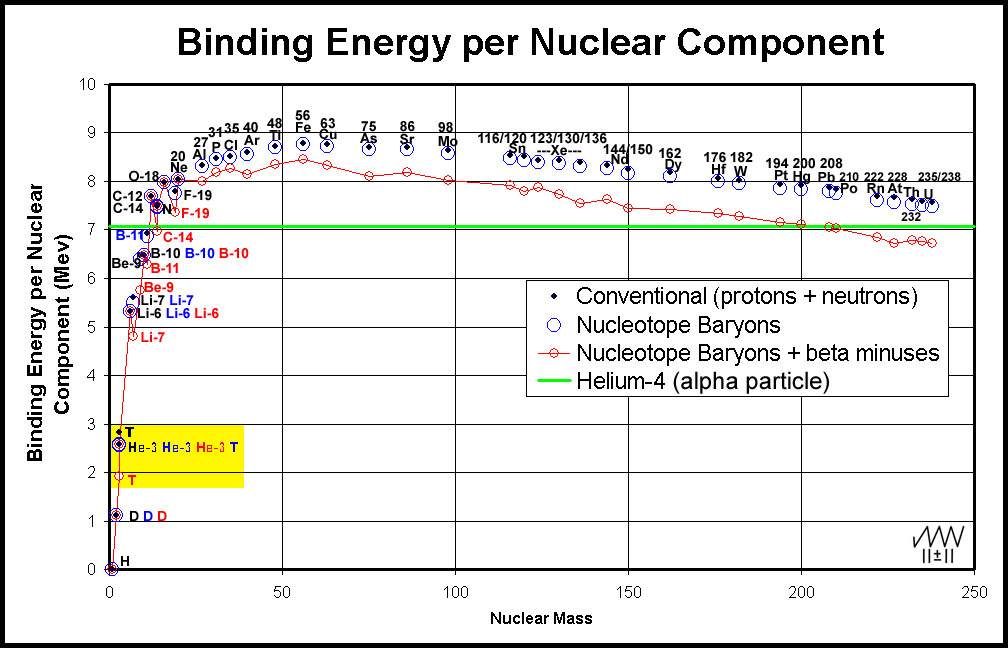
Figure 9. Binding Energy of Elemental Isotopes per Nuclear Component
Attention is drawn to the trio of T and He-3 entries in the yellow rectangle in the lower left of Figure 9. The conventional determination of the binding energy (black dots) for tritium (T) and helium-3 (He-3) gives the binding energy per baryon of T greater than that of He-3. This is strange considering that T → He-3 + β- + energy. The enigma, of course, lies in the choice of starting nucleons.
In the conventional model, the nucleus has only baryons: protons (charge/atomic number) and neutrons (additional mass).
T (1p+2n)conventional = 3.0246 amu; He-3 (2p+1n) = 3.0232 amu. Ending measured element masses less the valence electrons: T = 3.0155 amu; He-3 = 3.0149 amu; ∆ = 0.0006 amu (the mass of a
β- + some energy).
In the nucleotope model, a β- particle is included and the number of each baryon is reversed with the result that the binding energy of T and He-3 are approximately the same per baryon ― blue points in Figure 9.
T (2p+1n+1e)nucleotope = 3.0238 amu; He-3 (2p+1n) = 3.0232 amu. Ending measured element masses less the valence electrons: T = 3.0155 amu; He-3 = 3.0149 amu.
If, with the nucleotope model, however, binding energy is expressed per nucleon (2p +1n +1β-), the value for T is less than that for He-3, as expected for T → He-3 + β- + energy ― red points in Figure 9.
Further examination of Figure 9 shows that, while the binding energy per nucleotope nucleon is less than that per baryon, significant "corrective" measures like that for tritium only occur for masses below 19 amu where a few β- particles in a nucleus of baryons makes a large difference in the nucleon number. Maximal bonding occurs at Fe regardless of the methodology.
Why do Elements above Lead release α-Particles?
Unstable elements that occur above the "stability zone" and have atomic numbers less than 82 (lead, Pb) decay mainly by β- release. Elements with atomic numbers greater than 82 decay by α-particle (He-4 nucleus) release. While the binding energy of nuclei decreases after a maximum at Fe, there seems to be little rationale for this behavior in the conventional, proton/neutron model. Inspection of Figure 9, indicates that the binding energy of these nuclei is well above that of the helium-4 nucleus (see the black dots versus the green α-particle line). When binding energy is determined per nucleon and the nucleotope model, however, the reason for α-particle release becomes clear. Lead (Pb-82) is the highest atomic number/mass element that is stable. It is also the last element whose nuclear binding energy/nucleon is greater than that of helium-4. Beyond Pb, the binding energy per nucleon dips below that of Helium-4 (the α-particle). Elements with atomic numbers greater than that of Pb are α-emitters as this more stable chunk of baryons breaks away from the more poorly bound nuclei. The process continues until the binding energy/nucleon of the nucleus is greater than that of the α-particle. This often occurs when the sum of the emitted α-particle chunks reduces the mass to Pb-82. That α-particle release by these elements occurs is not at all surprising with the nucleotope model.
References
1 Standard Model: (a) M. Gell-Mann, Phys. L&t. 8, 214 (1964); (b) G. Zweig, An SU3 Model for Strong Interaction Symmetry and Its Breaking, CERN Report No. TH 412 (Geneva, 1964);__ (b) Feynman diagram: β+ decay of a proton into a neutron, http://hyperphysics.phy-astr.gsu.edu/hbase/forces/funfor.html
8 Joel M Williams, Creating the Familiar Periodic Table via MCAS Electron Orbital Filling, http://pages.swcp.com/~jmw-mcw/The Familiar Periodic Table of Elements and Electron Orbital Filling.htm 9 Joel M Williams, The MCAS Electronic Structure of Atoms, http://gsjournal.net/Science-Journals/Essays/View/4019; discussed in The spdf Electron Orbital Model Parsed, http://gsjournal.net/Science-Journals/Essays/View/5032 10 Exact Masses and Isotopic Abundances; http://www.sisweb.com/referenc/source/exactmaa.htm 11 Similar plots for the conventional approach: