Avogadro's Number Needs A Simple Expression
Joel M Williams (Dec 2013)
Spheres of crystal silicon are touted as the new standard for weights and measures.
For "Crystalline Carbon and Silicon: Covalent or Ionic?" (click here)
Avogadro's Number
Needs A Simple Expression
Joel M Williams (Dec 2013)
Spheres of crystal silicon are
touted as the new standard for weights and measures.
For
"Crystalline Carbon and Silicon: Covalent or Ionic?" (click here) 

|
is a 18-chapter, 164 page paperback compilation of articles by JMW $19.95
US list at Amazon
|
Abstract
ALL of
the methods to determine Avogadro’s Number should give the same value! With x-ray crystallography
commanding the quest since the 1930's, the value has dropped. A plot of some of
the values generated by different methods is given. A reciprocal change in
Planck's Constant is discussed. A very simple 'power-of-two" is proposed to
define Avogadro's Number as a constant with a value between the old and the
currently accepted.
DISCUSSION
A brief look at the changes in the value of Avogadro's number with time and methodology is given in the figure below with the sources listed in a table further on.
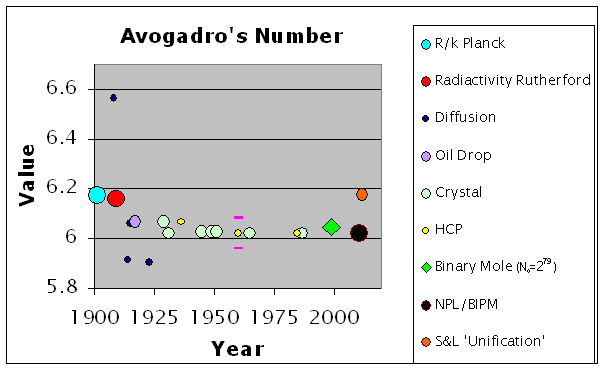
The crystal and NPL/BIPM values are driven by the definition of the kilogram with the HCP values following suit. Other than the widely variant diffusion values, the values from the other approaches indicate that the x-ray derived values are too low.
ALL of the methods should give the same value of Avogadro’s Number!
The numbers of 28Si atoms in those highly polished, "kilogram" spheres are certainly well-determined. With the "proper" value of Avogadro’s Number defining a mole, and a periodic table "element' standard (why not the 28Si that make up those spheres?), a "proper" value of the kilogram can be obtained.Redefining the kilogram via [Kilogram → x-ray Avogadro's Number → Kilogram] is circular reasoning.
A good history of Avogadro’s Number is at: http://depa.fquim.unam.mx/amyd/archivero/Avogadro%5C's_Number_17614.pdf
Also (Feb 2013) http://www.nist.gov/director/vcat/upload/International-Metrology-and-the-Redefinition-of-the-Kilogram.pdf
Consensus?
| Year | Source | Method | Value / 1023 |
| 1873 | J D van der Waals | Early | 11 |
| 1908 | J Perrin | Early | 6.7 |
| 1914 | T Fletcher | Early | 6 |
| 1890 | W RRontgen | Film | 7 |
| 1890 | J W S Rayleigh | Film | 6.08 |
| 1924 | PL du Nouy | Film | 6.004 |
| 1901 | M Planck | R/k | 6.175 |
| 1909 | E Rutherford | a-particle theory | 6.16 |
| 1908 | A Einstein | Diffusion theory | 6.56 |
| 1914 | I Nordlund | Diffusion in fluids | 5.91 |
| 1915 | A Westgreen | Diffusion in fluids | 6.06 |
| 1923 | TWShaxby | Diffusion in fluids | 5.9 |
| 1903 | HA Wilson | Oil drop method | 9.3 |
| 1904 | J JThomson | Oil drop method | 8.7 |
| 1917 | RA Millikan | Oil drop method | 6.064 |
| 1929 | R T Birge | Crystal | 6.064 4 |
| 1931 | J A Bearden | Crystal | 6.019 |
| 1945 | R T Birge | Crystal | 6.023 38 |
| 1949 | M E Straumanis | Crystal | 6.024 03 |
| 1951 | JWM DuMond | Crystal | 6.025 44 |
| 1965 | J A Bearden | Crystal | 6.022 088 |
| 1987 | R D Deslattes | Crystal | 6.022 134 |
| 2011 | NPL/BIPM | Crystal (kilogram & 28Si) |
6.022 140 78 |
| 1936 | Handbook Chem & Physics | 6.064 | |
| 1960 | Handbook Chem & Physics | 6.02 | |
| 1985 | Handbook Chem & Physics | 6.022 045 | |
|
1996 |
JM Williams Binary Mole | Halving decay to whole unit | 6.044 629 098 073 145 873 530 88 |
|
2012 |
Seshavatharam &
Lakshminarayan http://vixra.org/pdf/1209.0106v1.pdf |
"Unification?"
Rest mass - Gravity |
6.174 407 621 |
Note the near identity of Millikan’s 6.064 1917-oil drop value, and Birge’s 6.0644 1929-crystal value; the 1936 HCP reflects these. Note, now, the 0.041 drop in Birge’s 6.0644 crystal value to 6.02338 in 1945. The change from the oxygen standard to carbon-12 did not occurred until 1967 with the International Committee for Weights and Measures and until 1971 with the General Conference on Weights and Measures. Avogadro’s Number then began to hone in on 6.0221. Not surprisingly, the current 2010 CODATA Faraday (coulombs/mole) divided by the current e-charge (coulombs/electron) give 6.022 141 293, as the mole is based on the current definition of the kilogram and thus circular reasoning.
There is much intertwining of physical property values with Avogadro’s Number being common to many. Hence, “adopting a concrete value” for some properties forces other properties to have “preordained” values. Avogadro’s Number has thus been “directed”.
Planck’s “constant” was “1.2% greater” in 2010 (6.62606957(29) ×10−34 Js: 2010 CODATA) than it was in 1901 (6.55 ×10−34 Js: copy of Planck’s paper at http://bourabai.kz/articles/planck/planck1901.pdf); their ratio and the current Avogadro’s Number give an Avogadro's Number of 6.092 that is in line with values (6.1; average of Planck, Rutherford, Millikan, Birge) until the 1930s. It is interesting that, while Planck's papers in the early 1900's are referenced in Steiner's history (http://iopscience.iop.org/0034-4885/76/1/016101/pdf/0034-4885_76_1_016101.pdf), Planck's 1901 Constant value is not plotted in Fig 2 of that reference that spans 1900 to 2020. I have reproduced Steiner's Fig 2 and added Planck's value in the following figure.
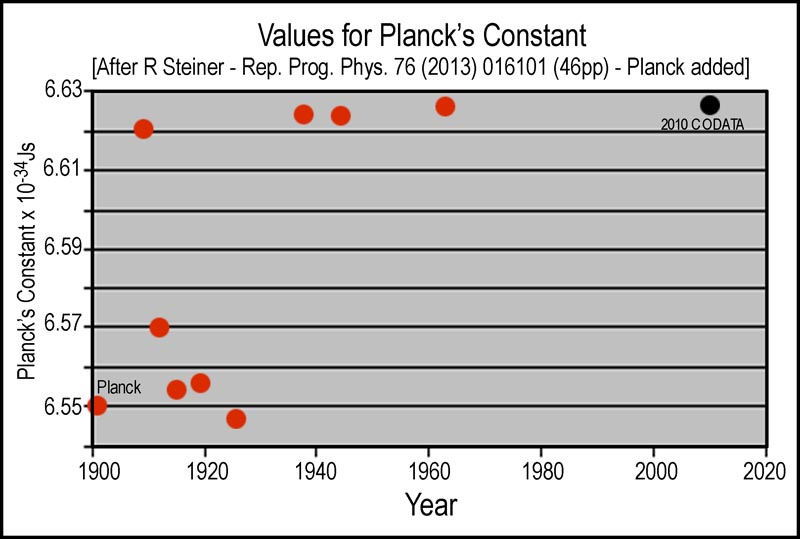
The plot of Planck's Constant (E=hc/λ) values in Js (m2kg/s) with time and the plot of Avogadro's Number earlier indicate that these two physical "constants" have simply been reciprocally changed: new product/old product = [(6.62606957*6.022141)/(6.55*6.1)] = 0.999. Did Planck also make a mistake as has been attributed to others before the jump in Planck’s Constant around 1930 in the history account? Again, the issue is all about the definition of the kilogram.
Considering all of the changes in many of the physical units over the
last century,
I
suggest that Avogadro’s Number, thus the mole,
be a very
simple expression
and have a value between the old and current values.
No = 279 is such an expression.
Its full value is
6.04462909807314587353088E23 for the fine
stuff and standards
while 6.0446E23
is for the rough stuff.
Polished 28Si marbles would be distributed to standards labs and balance manufacturers defining the "new K".
Experimentally measured properties can then fall in step.

A
note about integer quantities
A dozen is a set integer count of things - (12) - whether it is eggs, rolls,
balls, screws, nuts, etc. Suggesting that the size of the eggs should influence
the count in a dozen would get a response of rolling eyes and a shaking head
from anyone with much of an IQ.
A dozen large eggs should be 12.5 while a dozen small eggs should be 11.5?
Ludicrous. The difference would be in weight not numbers.
In many ways, however, that is what has been occurring over the past century
with the definition of the mole.