

Joel M. Williams
Los Alamos, New Mexico 87544
©2001 JMC Williams Consultants
(this is the full image version of the one in the arxiv database)
A PARTICLE APPROACH TO THE ELECTRONIC BEHAVIOR OF ATOMS AND MOLECULES
ABSTRACT
The spdf-based atomic and molecular orbital theory is a sophism. Duality is based on the electrostatic property of an electron being substituted for the whole. The additivity of the property is used to justify the additive of the whole. In this way, electrons can statistically occupy the same space at the same time. The non-additivity of like-charged particles and the particles themselves vanish in directed logic. Reverent fostering perpetuates the stratagem. The homophilic electron gets praised as the creator of all things. Things are declared to be different at the electronic level and that classical physical laws do not apply. This paper shows that classical physics is still alive and well down at the electronic level! Electrons are particulate as long as they remain electrons; i.e., there is no mass-energy reversal on demand. Duality, as currently asserted, does not exist for an electron and is, thus, flawed logic.
MCAS is an acronym for the orbitals [Multilobed (tetrahedral), Cubic, Anticubic, and Square-faced cubic] of a particulate orbital approach. The MCAS approach explains the behavior of an electron with classical physics that maintains the integrity of the particle. The electrostatic fields from electrons are additivity, but the probabilities of electrons occurring in the same space are mutually exclusive and, therefore not additive! That is, two electrons are not allowed to harmoniously share the same orbital space at the same time ¾ electrostatic particle orthogonality. Beyond this, the MCAS approach should yield to mathematical treatments in much the same way the spdf-based theory does. The MCAS approach demonstrates that atoms are indeed "the building blocks of nature".
This treatise details the electrostatics of some simple molecules modeled the MCAS way. The orbital extent of an electron is finite! Its electrostatic presence, however, can be considered to stretch to infinity. An electron hardly ever occupies the region on the axis between two nuclei. Usually when this happens, the molecule is in an activated state. Excellent correspondence of NMR proton shift with the magnitude of the electrostatic field at the proton is found.
Wholly integer quantum numbers are assignable to each orbital space of an atom. Electrons do not have quantum numbers! The acronym "stogh" (pronounced stow) stands for shell (1-n), type (1-4), orthogonality (1 or –1), group (1-k), and ‘home’ (1-m). The electron of the hydrogen atom is assigned the 11111 orbital; those of helium are in the 11111 and 11-111 orbitals; and so on. Each electron is assigned to a separate ‘home’ orbital in a group, although they may alternately roam the orbitals within the group. Unlike the static spdf designation, an electron moves to a different type (M, C, A, or S) of orbital with sufficient electron loading of a shell!
The MCAS way describes the behavior of electrons while preserving their wholeness, mutual orthogonality, and interactive adaptation. Inter-atom attractions and repulsions without spin-paired electrons on the direct line between nuclei properly explain bonding between atoms. Ionic and covalent bonding are explained by the same electrostatic rules. Classical physical laws continue down to at least the electronic level!
A description of SN2 organic reactions based on the MCAS electronic structure of atoms and molecules is given. The concept of microscopic reversibility in the Transition State of SN2 reactions is trashed.
PREFACE
This paper contains extensions and applications of the MCAS (an acronym for 3-D orbital types: Multilobed (tetrahedral), Cubic, Anticubic, and Square-faced cubic) approach to atomic and molecular orbitals. It is broken up into four parts, several of which have their own Introduction and Summary.
MCAS Models
This part provides a brief overview of the MCAS approach to atomic orbitals and molecular bonding.
INTRODUCTION; ORBITALS THE MCAS WAY; BULLIES, WIMPS, and the REST
SINGLE BONDS (HYDROGEN MOLECULE, CHLORINE MOLECULE, ETHANE)
TRIPLE BOND (ACETYLENE, NITROGEN MOLECULE); SUMMARY
Electrostatics for MCAS Models
This part provides electrostatic calculations for some MCAS-formulated molecules. Such electrostatic models would be impossible with current methodology because of electron-electron repulsion. Contour gradients are shown for a number of molecules. Correlations with NMR chemical shifts are made.
THE CUBE AND THE SPHERE; The SIMPLE SIGMA-Xi BOND
ELECTROSTATIC CALCULATIONS
ELECTROSTATIC PLOTS (HYDROGEN MOLECULE, CARBON DIATOM, NITROGEN MOLECULE,
OXYGEN MOLECULE, FLUORINE MOLECULE, NEON ATOM)
PNMR SHIFTS AND FIELD INTENSITY; SUMMARY
Quantum Aspects
This part discusses atomic orbital description, why the current methodology is faulty, and provides new quantum numbers for stowing electron around the nucleus.
ONE ELECTRON PER ORBITAL - PAULI
MCAS QUANTUM NUMBERS
NO NEED FOR PARTICLE THEORIES?
Reactions the MCAS Way
This part provides a mechanism for SN2 reactions based on MCAS modeling. The mechanism involves an electron-transfer in the Transition State. As a result, microscopic reversibility can not occur and the concept is trashed.
MODELS and REACTION PATHS, MCAS MODELS OF SEVERAL ATOMS
MCAS versus Currently-Accepted MODEL OF METHYL FLUORIDE
MICROSCOPIC REVERSIBILITY IS NOT
SN2 REACTIONS THE MCAS WAY
PART I
The MCAS model of the electronic structure of atoms describes an orderly placement of the electrons around the nucleus without the need for electron spin reversal. This is achieved through opposing electron motion in nested orbitals that is equivalent to spin reversal. Major restructuring of a shell is part of the model when the electron load requires it. The energy to maintain an electron in an orbit/orbital is provided by its interaction with the nucleus ¾ synchronization between electron and nucleus being required; attraction and repulsion implicit.
Before proceeding, it is appropriate to comment on two issues: electron spin-reversal and orbital character. In the beginning, the creator flipped the great coin of the universe: heads to the right; tails to the left. Its fate determined, the matter of the coin spiraled outward. The hand (spin) of the electron determined as well - a base descriptor. According to current atomic and MO treatments [Current basic concepts of molecular modeling and atomic structure are found in chemistry texts, such as: Chemistry, Raymond Chang, Random House, New York; Introduction to Organic Chemistry, A. Streitweiser Jr. and C.H. Heathcock, MacMillan, New York; Advanced Inorganic Chemistry, F.A. Cotton and G. Wilkinson, Interscience, New York; and Physical Chemistry, F. Daniels and R.A. Alberty, Wiley, New York; their progeny and similar ilk.], reversing spin does not negate electron charge, but it does negate negative-negative repulsion - a hallucinative tenet. Do you profess belief? Why?
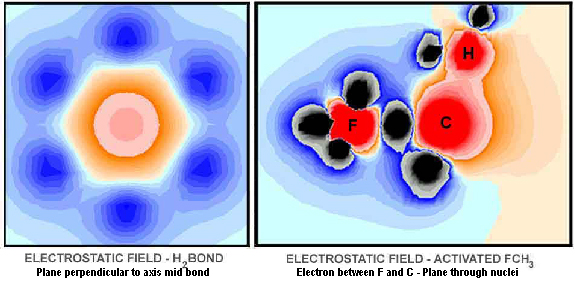
Electrons form synchronous units with nuclei. Spectral data dictate that the motions of electrons be precisely repetitive, not fuzzy; hence, finite and closed. The physical volume of an electron is tiny, but its duality component (electrostatic charge) radiates outward at 1/r2 to yield an electrostatic cloud. Figure 1 simulates the planar (to the paper) radiation for a nucleus (red) and for temporal locations of an electron (blue) in a four-lobed (tetrahedral) distribution. The electrostatic presence of an electron extends to infinity in all directions with an ultimate intensity of 1/(infinity)2 no matter where the electron might be. Spectral signature, on the other hand, defines a finite presence for an electron. The finite physical space occupied by an electron based on its spectral signature is more properly its orbital space. Electrostatic issuance is a boundless property, but electron presence (probability) is physically bounded.

Two electrostatic clouds are always overlapped; be they positive-positive, negative-negative, or positive-negative. Everything in the universe is electrostatically connected to everything else this way. Thus, an electron is somewhere in its and every other electron's electrostatic cloud at all times. Electrostatic repulsion will minimize overlap intensity, however. Methodologies that maximize negative-negative overlap are, thus, invalid; be they probability or particulate based!
Pairing electrons by opposing their movement requires neither spin-reversal nor maximized negative-negative overlap and, thus, provides an electrostatically allowable methodology. This is "The MCAS Way".
B. ORBITALS THE MCAS WAY
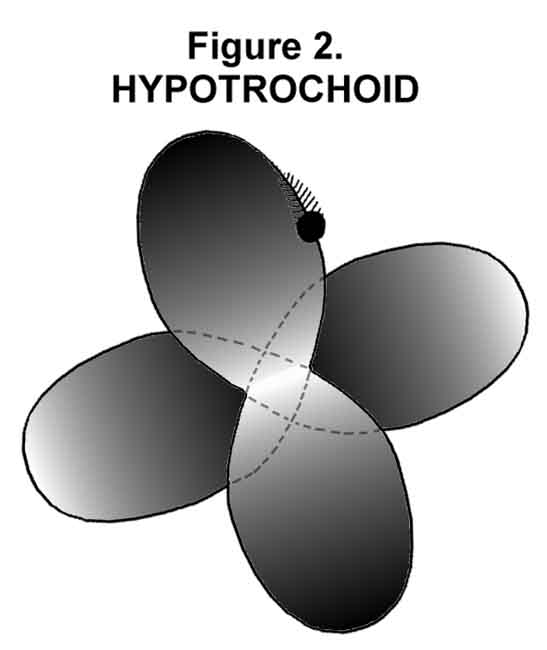
Every electron in the MCAS electronic model has an instantaneously separate orbital space. The most basic electron orbital is the M (multi-lobed) orbital. The motion in this orbital is a 3-dimensional version of a hypotrochoid (Figure 2) that yields a tetrahedrally disposed electrostatic cloud (Figure 1). Note that the nucleus can be seen and hence provides routes of attraction of another atom's electrons. This is in sharp contrast to the commonly accepted spherical s-orbital that should present a uniform negative picture to another atom! The mathematician can model either the spherical or tetrahedral distribution. Indeed, the M orbital is just like a sp3-hybrid orbital set, except that a single electron roams all four lobes. If you are squeamish about one electron traveling in more that one lobe, think about what happens in the p, d, and f orbitals of the current scheme.
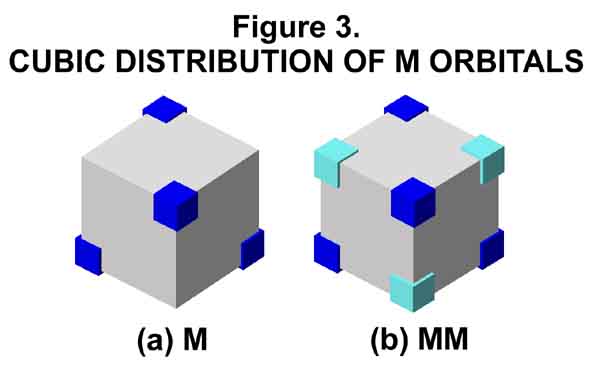
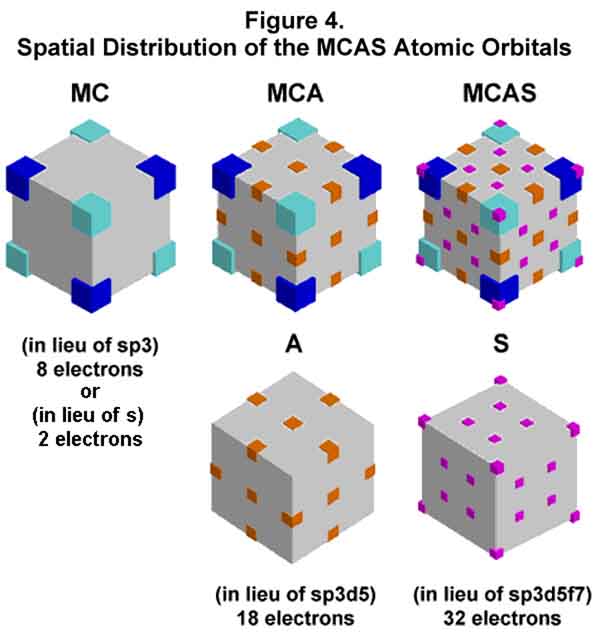
For ease of spatial comprehension, visualize [3-D modeling program: freeware downloaded from Artifice, Inc. at http://www.artifice.com] the M orbital as part of a cube (Figure 3a). Colored blocks (dark blue) located at the four diagonal corners of the cube indicate the orientation of the lobes. [Angular orbital shapes are not implied! The cubic depiction is a matter of graphic convenience.] Another M orbital (aquo blocks) nests with it to form the opposing electron motion (Figure 3b). When more electron density is required at a specified distance (energy level) from the nucleus, up to three more electrons can occupy the tetrahedral orbital space. This converts the M orbital (1 electron per tetrahedral orbital) to C orbitals (2 to 4 electrons per tetrahedral space, yet 1 electron per lobe). One M to C conversion completes before another begins; Hund's rule no longer needed. The electrons in the C orbitals interact synchronously with each other, with that (those) in the opposing M (or C) orbital(s), and with the nucleus. When even more electron density is required, the C (cube or corner) orbital configuration rearranges to the A (anticube) configuration wherein the lobes are aligned towards the center of the cube's edges (12) and faces (6). When even more electron density is needed, the A orbital configuration converts to the S (square-faced) configuration wherein the electrons' lobes are aligned towards the corners (8) and the faces (4*6=24) between those of the A configuration. Hence the electronic aufbau completed shell levels are 2 (M2), 8 (C8), 18 (A18), and 32 (S32) with every electron of a given energy level of a noble gas element being identical! The 3-dimensional spatial distribution of the lobes can be easily visualized with the help of cubes (Figure 4).
C. BULLIES, WIMPS, and the REST
The struggle for total electronic counterbalancing can be summed up this way: those that can take; those that can not cede or co-op. Thus, are born ionic and covalent unions. In the first three periods, the rule of 2 (M2) or 8 (C8) prevails; just like Lewis wanted, but with a different e-pairing scheme! The business at hand is to negate all unopposed electronic motions. In the ionic case, the opposing motion will be achieved by centering the motion about each individual nucleus. In the covalent case, the opposing motion will be achieved by centering it between the two nuclei. Note that it is the motion of the electrons and not the electrons themselves that is centered! Electrostatics requires that the two opposing electrons remain as far from one another as possible. Thus, the probability that they will form an elevated electrostatic presence on a line between two nuclei is 0. Covalent bond formation is now little different than ionic bond formation - both controlled by electrostatics and motion counterbalancing. Cooperative (covalently bound) atoms are more like self-satisfied couples and small groups that can cluster in large arrays if so ordered. Atomic bullies (anions) and wimps (cations), on the other hand, loathe their own and love their opposite. Satisfaction (electrostatic bliss) comes in the crystalline or solvated state.
D. SINGLE BONDS
The MCAS modeling of single bonds will be illustrated with the following three molecules: H2, Cl2, and CH3CH3.
1. HYDROGEN MOLECULE
The hydrogen molecule provides the simplest covalent bond. In the spdf molecular bonding concept, this occurs with two spherical orbitals merging while one of the electrons changes spin. Electrostatic density piles up between the nuclei, especially on the axis between the two. At least that is the implication, even if mathematical "spin" (color, whatever) is not physical spin - a leap of faith! In the MCAS bonding concept, two tetrahedral M-orbitals mesh with their electrons paired by counter motion. Truncated and untruncated cube models are shown in Figure 5. One M-orbital is shown in aqua to emphasize its reversed placement. As in the current concept, electron density is mainly between the nuclei as would be expected, just not on the axis. Positive-negative electrostatics is clearly operating in the MCAS approach. The driving force in the spdf approach escapes me. Electrostatics is the only interaction of concern here. No electron spin reversal is necessary, just spin opposition.
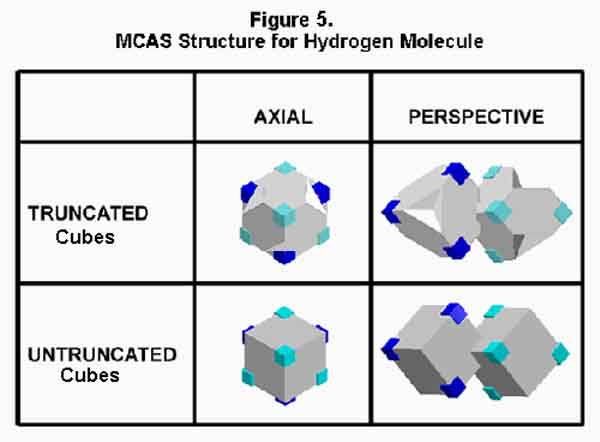
In the case of the hydrogen molecule, there are only two electrons and they will always be on opposite sides of the bond at any given time. Since the bond is actually formed by trigonal, epi-counterpoised orbitals, it should be called a Xi (X) bond. To emphasize its conventional sigma bond relationship, I choose to call it a sigma-Xi (sX) bond. The MO diagram should be like that in Figure 6 with each of the "x"ed arrows indicating a 1/4 electron presence. Note that the molecule has stability because there are NO repelling electrons in the sigma bond!
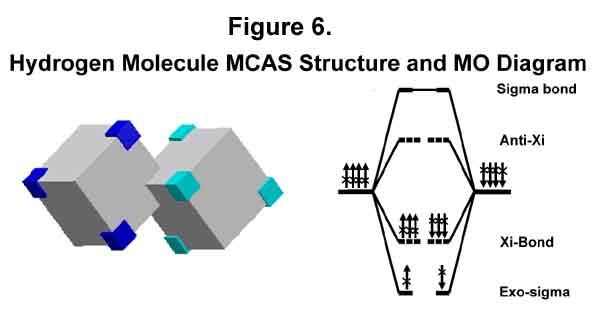
2. CHLORINE MOLECULE
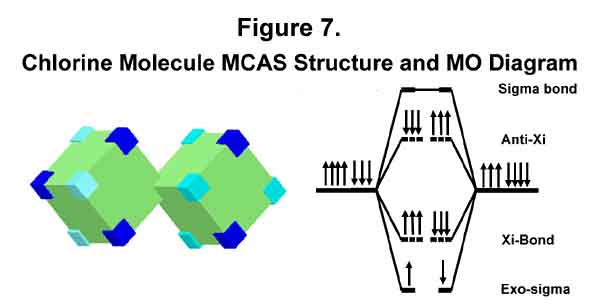
The MCAS structure of a chlorine atom’s valence shell is C4C3. A chlorine molecule occurs when two chlorine atoms minimize each other’s single electron deficiency. The MCAS structure and MO diagram are given in Figure 7. The similarity between the current MO notation and the MCAS MO notation is easily seen. Like that for the hydrogen molecule, however, the designations of the various levels are different. Bond destabilization to that of a single bond is provided by e-e repulsion between the six anti-Xi and the six Xi-bond electrons; otherwise the Xi-bond would be stronger. (Hold that thought!) There is no reason to expect the anti-Xi destabilization to cancel the Xi-bond electron-for-electron. It is convenient to express it this way, however, and to put the difference in the exo-sigma level designation. Lewis' dots are paired as he would want, but they are on opposite sides of the bond, not in it.
3. ETHANE
The carbon valence-shell electrons in the ground state are MC3. For single bonding in the alkanes, the M electron is elevated to give the symmetrical C4 state. [Total electron distribution looks like that of hydrogen (M).] The staggered MCAS conformation of ethane is shown from several vantagepoints in Figure 8. Blue and aqua colored electrons are used to indicate opposing electron placements. Orbital symmetry and maximum distancing of electron density is readily apparent.
The C-C single (sigma-Xi) bond of ethane is like unto that for the chlorine molecule (compare Figures 8 and 7). Three electrons from each carbon are involved in the Xi-bond. The fourth electron of each carbon is exo-counterpoised to the bond ¾ a feature seen in the hydrogen and chlorine molecules; the sigma bond is their opposite. Instead of the anti-Xi electrons that occur in the chlorine molecule, their CH Xi-bond replacements provide the e-e repulsion that reduces the strength of the C-C Xi-bond to that of a single bond. Thus, a B-arrow (bond) replaces the electron arrow in the MO. Of course, the B-arrow has a direction equivalent to the electron it replaces. The electrons involved here are the ones on the hydrogen atoms that form the CH bonds. Using the B-arrow notation indicates the situation more generally.
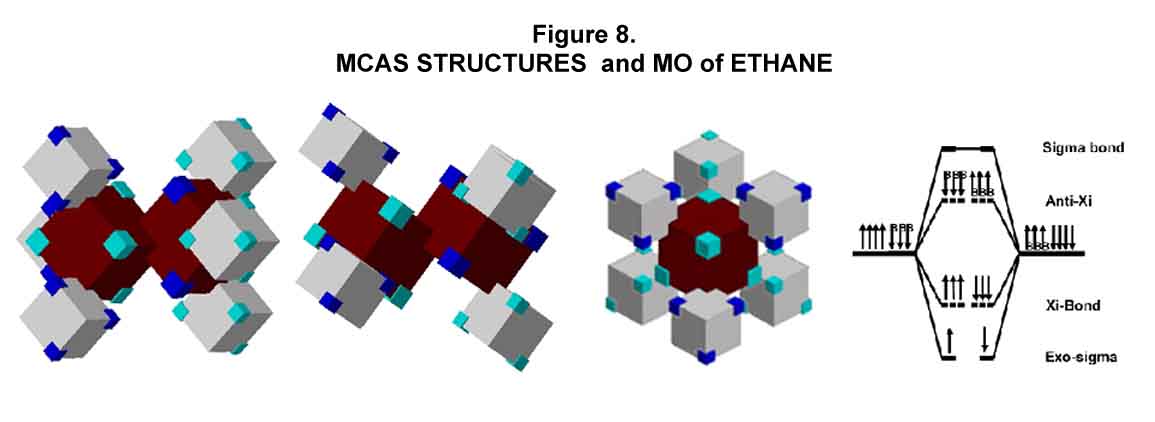
Resistance to rotation about the C-C single bond is typically attributed to interactions of electrons in bonds on either side of the C-C bond. In the MCAS approach, the resistance is due to the Xi-orbital interactions between the carbons. This is more in harmony with data that shows that the resistance to rotation about the C-C bond of ethane is not significantly different from that for the center C-C bond of butane. All of the single bonds in saturated alkanes are sigma-Xi (sX) bonds.
E. THE TRIPLE BOND
Multiple bonds are bonds that are significantly stronger than comparable sigma-Xi bonds that have six anti-Xi electrons or bonds. Triple bonds, in fact, are just especially strong sigma-Xi bonds. A triple bond has no P-type bonds!
1. ACETYLENE (ETHYNE)
The carbon valence-shell electrons in the ground state are MC3. The M electron is not elevated to a C electron in the case of acetylene. Thus, the electronic structure of the acetylenic C-C bond is much like that of the chlorine-chlorine bond, except that in this case only two M-electrons counter the six C3 electrons that form the sigma-Xi bond. The MCAS structure and MO diagram are given in Figure 9 with the carbon M orbitals dark blue. From this smaller e-e repulsion results the strength of the triple bond. Thus, a triple bond is just a special case of a tri-lobed sigma-Xi bond where there are only two anti-Xi electrons instead of six. Extra strength may also result if the orbitals about each carbon were to wax and wane alternately. The M electrons may also pass from one atom to the other.
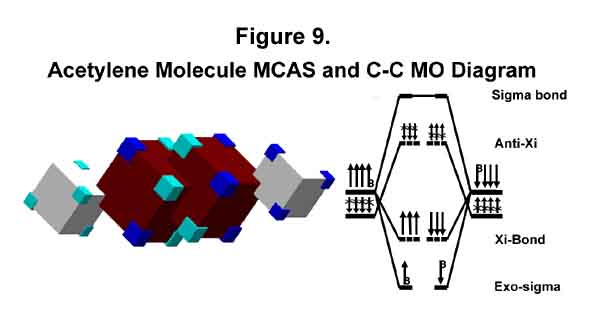
The M-orbital of acetylene is similar to its C counterpart that blooms out towards the hydrogen atom of ethane, except there is only one electron in the three lobes instead of three! This results in 1/3 the shielding that occurs in the saturated alkane case; hence acetylenic protons will look a lot like alkyl protons in NMR, but will be less shielded. [For a discussion of NMR, see Introduction to Organic Chemistry, A. Streitweiser Jr. and C.H. Heathcock, MacMillan, New York [especially the discussion on acetylene (p304 - 1976 version)]; similar general texts or specific NMR texts.] No fancy hand waving is needed and the hydrogen atoms at BOTH ends of acetylene look just alike!
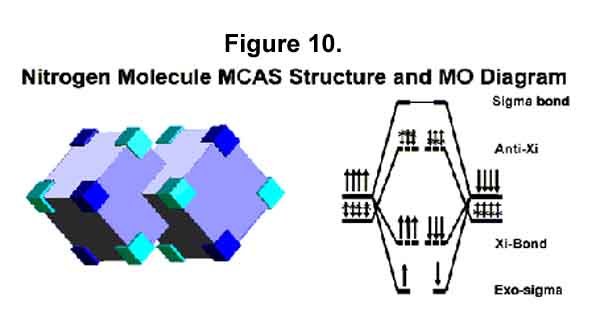
2. Nitrogen Molecule
The nitrogen valence-shell electrons in the ground state are MC4. The nitrogen molecule will look like the acetylene molecule with each carbon-hydrogen sigma-Xi bond replaced with an electron. See the MCAS structure and MO diagram in Figure 10. The lower energy M-orbitals have been left dark blue here to emphasize them. Again, only two anti-Xi electrons oppose the six Xi-bond electrons. There may be interatom transfer of the M electrons and alternate waxing and waning. Thus, N2 is a very compact bundle with a minimally destabilized sigma-Xi bond that has triple bond strength.
F. SUMMARY
Covalent and ionic bonding should both be covered by the same rules. The difference should be degree, not kind. The MCAS Way shows that they can, indeed, be explained similarly! With the MCAS approach to atomic orbitals, electron spin-reversal and doubly occupied orbital overlap are eliminated! Both of these concepts should repulse; yet they opiate - so venerated.
The situation for double and conjugate bonding is a little more involved than the single and triple bond cases shown in this paper, but they are still governed by electrostatic interaction. For these, some inorganic groupings like CO3=, NO3-, SO3, some involving phosphorous (P4, P4O6, P4O10) and boron (B2H6, B6H6=), and other single and tripled bonded molecules, the reader is referred "The MCAS Way" (1999) by the author. It can be inspected at http://arxiv.org/html/physics/9909053.
PART II

A. INTRODUCTION
The MCAS model of the electronic structure of atoms describes an orderly placement of the electrons around the nucleus without the need for electron spin reversal. This is achieved through opposing electron motion in nested orbitals that is equivalent to spin reversal. The outer shell of an element will normally have its period's noble gas maximum number (2 or 8) of electrons or less. Inner-shell packing is by uniform spatial allotment of orbital space between these orbitals. MCAS is an acronym for the orbital types that occupy 3-D space: Multilobed (tetrahedral), Cubic, Anticubic, and Square-faced cubic. For more on the MCAS methodology and the interplay of these orbitals, the reader is referred "The MCAS Way" (1999) by the author. It can be inspected at http://arxiv.org/html/physics/9909053
This section was initiated to provide mathematical support for the MCAS methodology. Before embarking, however, G.N. Lewis deserves a bit more credit than he has been given in the past.
B. THE CUBE AND THE SPHERE
G. N. Lewis made some of the earliest depictions of atoms. In doing so, he recognized the significance of the OCTET. The logical expression of an octet in 3-D space is a cube. Lewis used [Lewis, G.N., "Valence", Dover Publications, New York (1966)] one to represent his atomic structures in 1902 (Figure 11 - a rendition of Lewis' originals by this author). It is interesting that he depicted helium ("He") with "8" positions. However, since he also suggested that the indicated structure might be the "basis" for the "Na" row, it is more probable that he was thinking "Ne", not "He", when he wrote "Helium". It is not clear what he had in mind for the "kernel" in "C/Si". It is clear, however, that Lewis was not concerned about 3-D placement of electrons as he filled the "left" plane first and then the "right", with electrons placed next to one another. The exception, interestingly, is carbon/silicon! The significance of his depictions, however, is that when a shell is complete, all electrons will be alike! The author's MCAS model shows how electrons are placed orderly in this network to effect 3-D symmetry and spin-pairing. For Helium, the "black" and "white" tetrahedrally directed orbitals [designated M (multilobed) orbitals] contain one electron each. Hydrogen has just one M-orbital. With more than one electron, the tetrahedral M-orbital space becomes four C orbitals. MCAS orbital designations are given in Figure 11 for each atom. The C4 states for Carbon and Silicon are elevated, as M1C3 is the ground state.

In 1913, Bohr [Bohr, N, Phil. Mag., 26, 1, 476, 875 (1913)] introduced his spherical model of the hydrogen atom. In 1916, Lewis [Lewis, G.N., J.Am.Chem.Soc., 38, 762 (1916); also Lewis, G.N., "Valence", ACS Monograph Series (1923)] , departing from his cube representation, proposed the familiar valence-bond octet structure wherein electrons pair to form a bond between atoms; so intent was he on surrounding atoms with 8 electrons. Schrödinger [Schrödinger, E., Ann. Phys., 81, 109 (1926)] and Pauli [Pauli Jr., W., Z. Physik, 43, 601 (1927); CA, 21, 3309f (1927); b) Pauli's Nobel Prize speech about the exclusion principle is in Science, 103, 213 (1946)] sealed the fate of the spin-paired, overlapped, double-electron orbital and subsequent bond between atoms. Scientists of the 20th century never looked back - too bad. Skillful mathematicians could/would have modeled anything. [The classical, mathematical modeling case involves the earth-centered versus sun-centered universe. Both were modeled. Neither, as it turns out, was correct concerning the universe! If righteous electrons can remain chaste in the presence of attractive protons, are they repulsed by their sinister brethren down in the little nukey?] As it was/is, the homophilic couplet got sanctified. Humans have free choice, but I was not aware that electrons do.
A significant feature of the original Lewis cubic representations was that no two electrons occupied the same space. Indeed, Pauli's exclusion principle should have been just that. (Actually, Pauli also had one electron per box ¾ one oriented with the field and one against. He did not specify spin reversal, but spin opposition ¾ the basic feature of the MCAS approach.) Instead of securing a model that would do this, the mathematicians simply modified their mathematics to allow two electrons to share the same space with different "spin" numbers. Pauli was happy and other reservations, if there were any, drown in the wake of the power(ful) surge.
Lewis' valence-bond octet followed the principle that an atom tries to surround itself with eight electrons. The octet rule should have been that "an atom tries to cover eight positions". Coverage does not require two electrons directly between the atoms! Indeed, the electrostatic repulsion of two electrons in the same space would preclude two electrons from occupying the same, or generally same, space at the same time! The MCAS Way covers positions without this whimsy.
C. THE SIMPLE SIGMA-Xi BOND
Fluorine is the least electron deficient atom (of those deficient) in the list of Figure 11. The MCAS method for alleviating this deficiency is for two fluorine atoms to combine as depicted in Figure 12.
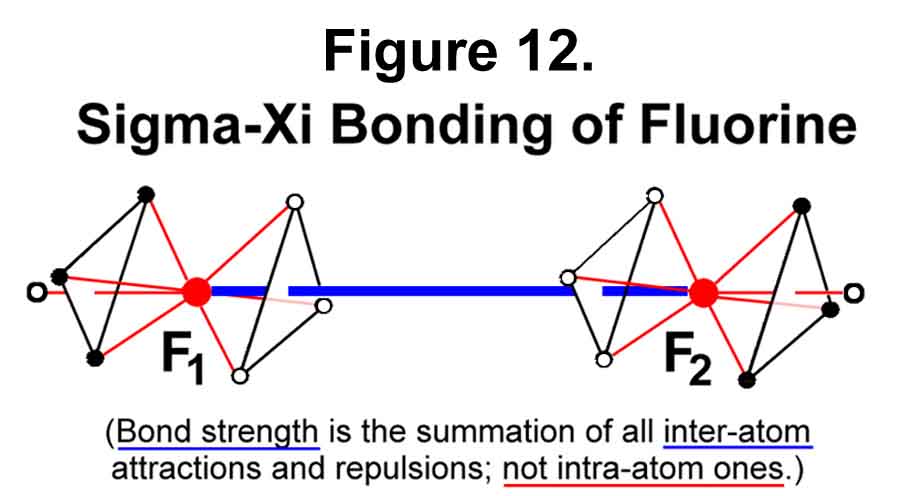
The bond between the two atoms is created by the attraction of the positively charged nucleus primarily on THREE of the other atom's electrons. For this reason, it is dubbed the "sigma-Xi" bond. This sigma-Xi bond is weakened by the repulsion between the electrons of one atom and those of the other and by the repulsion between the two nuclei. The eighth position of each atom is thus "covered". The axis (the traditional sigma bond) contains the non-bonding orbitals! Electrons are paired as "opposites" across the center of the bond.
The same bonding depiction can be made for H2. In this case, no black positions are filled and a single electron occupies the four white positions of each atom. For O2, the three black positions of each atom are occupied by an electron 2/3rds of the time; hence the observed unpaired electron character of O2. For N2, the black positions of each atom are occupied by 1 electron (mirror-imaged). A similar situation occurs for the C2 portion of acetylene where the two electrons opposite the bond are replaced with sigma-Xi bonds to hydrogen atoms.
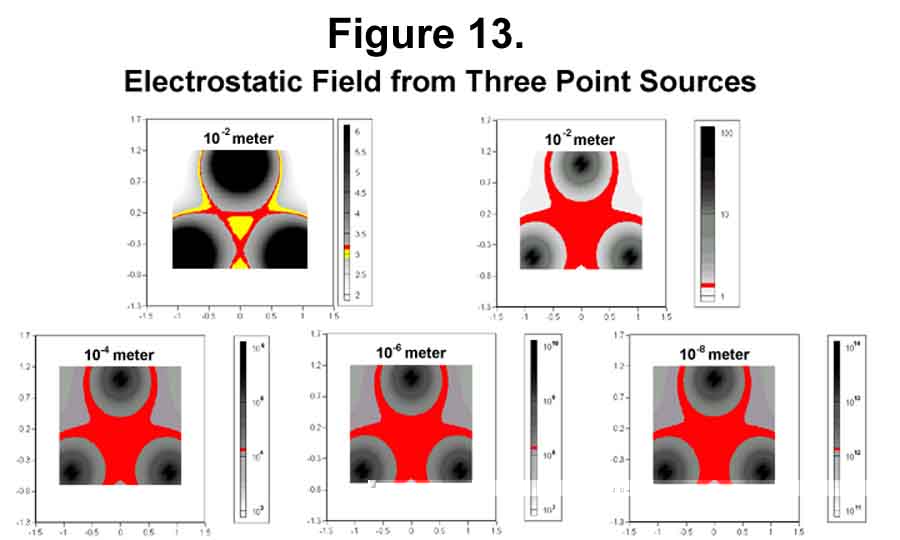
The three lobes of the sigma-Xi bond pose some interesting electronic effects around the bond axis. The electrostatic distribution of three lobes about the axis is the same regardless of their distance for the axis (Figure 13). The difference is in the magnitude. Because of the inverse square relationship, there is a minimum in the center. Surrounding the center is a crater-like rim that serves as a centering mechanism. The minimum and rim edge are more easily seen in Figure 14. The correct angle for the electron movement from a point for tetrahedral distribution is 70.52° . Because of differences in the x and y scales (y 1/2.8th that of x), the density in Figure 14 appears to fall off less rapidly along the axis than it actually does. Beware of graphic deception!
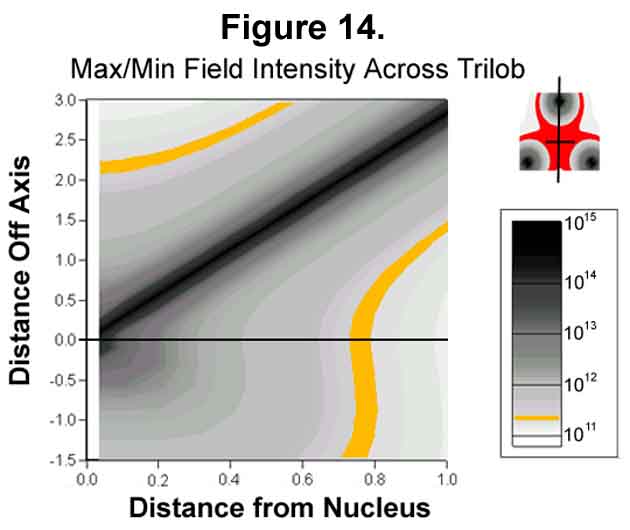
D. ELECTROSTATIC CALCULATIONS
Electrostatic calculations for sigma-Xi bonds were determined for H2, C2 (triple bond), N2, O2, and F2. Atomic distances were set to the published values. From this, the distance the electrons of the MCAS model could move outward at 70.52° before repulsion terms exceeded attraction terms was determined. Figure 15 illustrates the exercise for fluorine. (for clearer viewing, eXcel files are available of Figs 15, 16, and 36.)
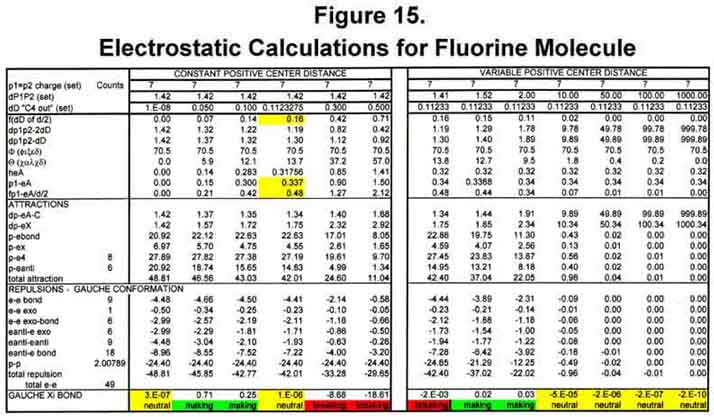
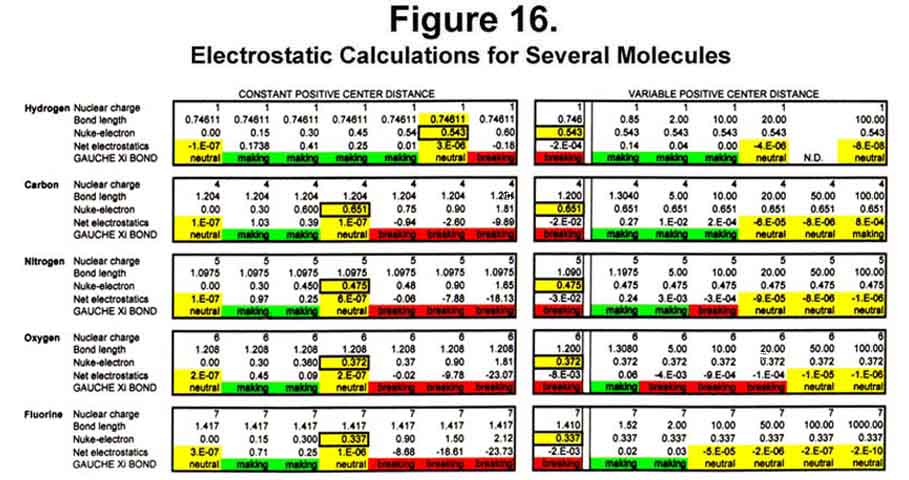
For the purposes of the calculations, the two first-level electrons were always assumed to be near the nucleus and therefore neutralized two charge units. They are not always there, however, as all electrons move in and out in unison to form the electronic beat. To insure that the calculations would start correctly, little or no bond forming tendency was established when ALL electrons were very close to the nucleus - a null, hypothetical case. As the valence electrons moved outward, bond making was favored to an early maximum and then tapered off to a "neutral" point. This "neutral" point was established as the outmost extent of the electron movement (orbital). Bond length would be determined by the outmost extent of the electron movement, not the other way around! If the electrons moved further out, the bond would be destabilized. To determine whether bond formation was favored at a distance, the electron extension for "neutral" bond formation was held constant and the atoms moved apart. As seen for fluorine, bond formation is favored at short separations, but is essentially neutral (slightly repulsive) as greater distances. Figure 16 shows the essence of the activity for H2 (M-M), C2 (MC3-C3M), N2 (MC4-C4M), O2 (C2C4-C4C2), and F2 (C3C4-C4C3), where the information in parentheses is the MCAS electron states of the atoms involved. Movement of the nuclei together at the outmost extension of the electrons destabilizes the bond (see the first column in the "Variable Positive Center Distance" portion). That the hydrogen orbital extent (0.543Å) is just half the typical C-H bond length is probably more than coincidental.
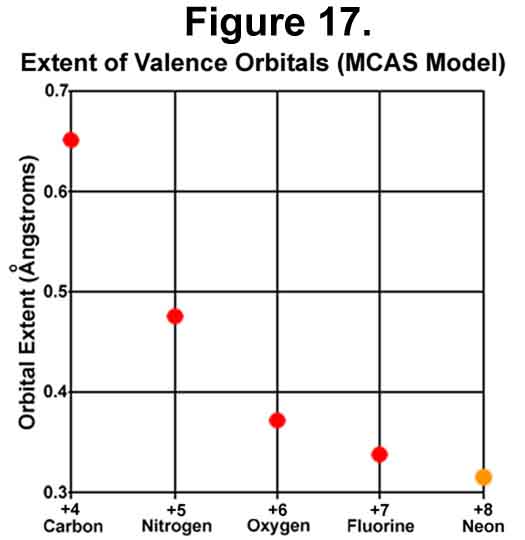
The distance between the nucleus and the electron outward motion decreases as would be expected with increasing nuclear charge (Figure 17). Neon is estimated from the general trend.
E. ELECTROSTATIC PLOTS
The 3-D electrostatic fields of some simple molecules were determined. The methodology involved first setting the atomic components (nuclei and their electrons) staggered in 3-D space. Next, the electrostatic sum at various points on a plane, such as through the bond axis, across the bond axis mid-point between the nuclei, or through a nucleus perpendicular to the bond axis was determined. Electrons were assumed to extend without distortion at 70.52° to the distance determined in Figure 16. Non-valence electrons were assume to be near the nucleus and reduced the nuclear charge by their number. Once the electrostatic sum at each point on the plane was determined, a contour plot [generated by SPSS DeltaGraph software during a 30-day review. The author found this program quite easy to use and the contour output nicely manipulable. The figures were made with Adobe Photoshop 4.0.] was prepared. Planes were especially chosen to pass through the atomic components. Although 500-1200 points were usually used, some non-smoothness occurred where the contours were particularly steep. This should not detract from the understanding of the situation. Determinations were made for H2, C2, N2, O2, F2, and Ne.
1. HYDROGEN MOLECULE
The hydrogen molecule is the simplest of molecules. In spite of this, the second electron has proven difficult to handle with current quantum theory methodology. With the MCAS model, the M-electron on each atom occupies tetrahedral space, which are placed with the tri-lobes staggered. Each lobe has an effective charge of -¼ ¾ elementary probability. The electrostatic field through the bond and four of the lobes is shown in Figure 18. The electrons do not extend far enough to transfer to the other atom. Indeed, there may be too much emphasis on electron transfer. Neither do they cover all the space close to their own nucleus; ergo, positive zones ("handles" for reaction events) for the hydrogen molecule (and atom), if the interaction distance is not large. In general, the molecule is broadly bathed in negative charge and, therefore, has some innate stability towards other molecules. Unlike the current spdf-derived model, there are no electrons on the internuclear axis. There is a greatly diminished positive field at the mid-point of the bond, however. The bond is stable because positive-negative attractions match repulsive interactions.
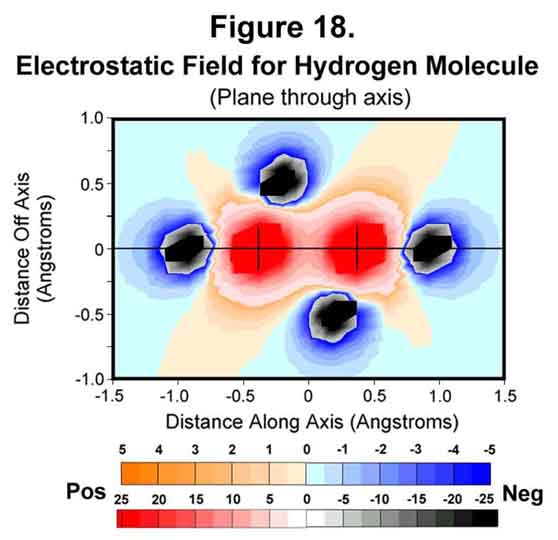
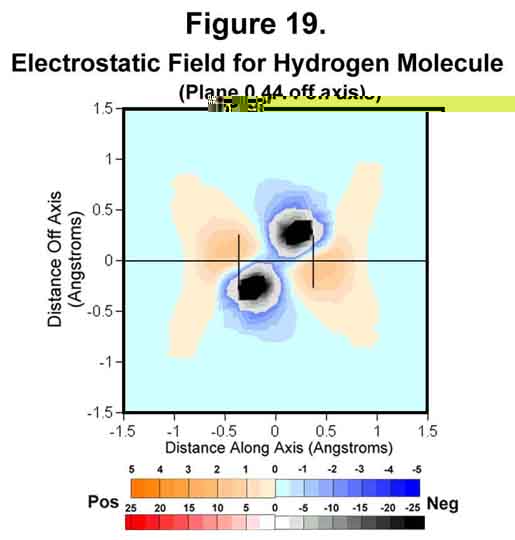
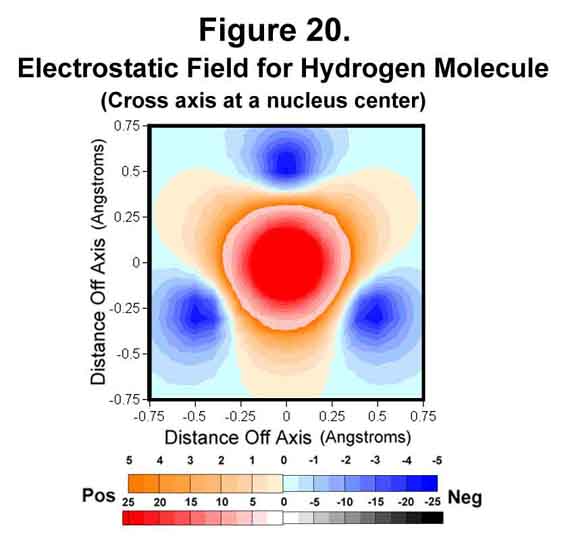
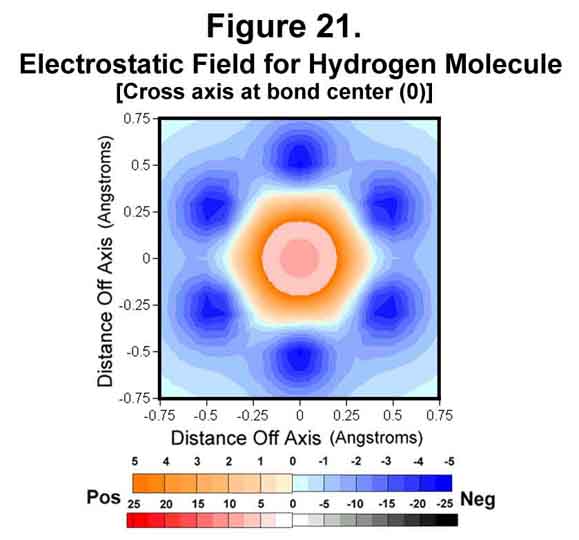
Some other perspectives of the electrostatic field are provided in Figures 19-21. Figure 19 shows the field through two of the sigma-xi lobes parallel to, but offset from, the bond axis. The field between the two atoms is very negative at this point! Figure 20 shows the trigonal field through the cross-axis of one of the hydrogen atoms. Figure 21 shows the field cross-bond midway between the two nuclei. As would be expected, the meshing tri-lobes have formed a uniformly symmetrical, hexagonal distribution of charge. This is for the staggered configuration, of course. Rotating the fields to the eclipsed position would require energy; hence, the observed rotational resistance for ethane and butane.
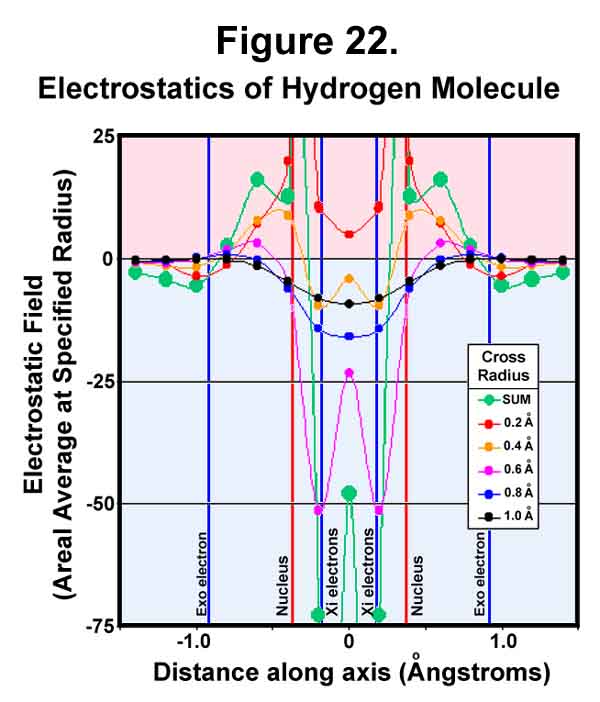
It can be argued that experimental evidence "proves" that electrons exist between the nuclei and, hence, on the internuclear axis. It is doubtful that electrons would stay there stationary for very long! In any case, measured negative electrostatic density does not necessarily mean actual electron presence! Figure 22 shows radial sums of the electrostatic field along the bond axis. The electrostatic sum was determined every 15° at the end of the specified radius and the sum of these values multiplied by the square of the radius to provide a cross-sectional value. The issue is "what is that 'experimental evidence' measuring?" If the experimental results show negative fields immediately over the nuclei, then the measurement is not close to the internuclear axis and the most intense negative field will be midway between the two hydrogen nuclei (see the pink, blue, and black curves where the radii are greater than 0.6Å). If the measurement is both for positive and negative fields, then the greatest negative field will again appear in the middle (the green "sum" curve). Only when the experiment is able to focus within 0.4Å of the internuclear axis (the red and orange curves) will the data not show a negative field concentration at the mid-point. All cross-sectional averages greater than this show a concentrated negative field at the mid-point of the H2 molecule. All this occurs without the actual presence of even one electron, much less two!
Actual electron presence in the sigma bond can occur (surely, to the delight of those who must have it so!) when there is significant difference in the effective "nuclear" charges of the two nuclei forming a bond. This occurs, for example, between carbon and fluorine of fluoro-substituted methanes (see NMR discussion, Part II-F). It occurs not because two high e-density orbitals are overlapped by spin-pairing, but, rather, because one electron of the less electronegative nucleus is drawn into its anti-sigma orbital at the expense of filling Xi-orbital space elsewhere. Significant redistribution of electrons may occur several atoms away. Similar effects would be expected in crystal field splitting by group 7 and 6 elements; much smaller ones by group 5 and 4 elements. The overlapped bond in the current quantum theory (QT) represents the probability of electron density being present. Since only one electron can occupy the bond space at any given time, the current QT needs to find a place for the other electron to spend while it is not in the overlapped region. The MCAS method has such places.
2. CARBON DIATOM
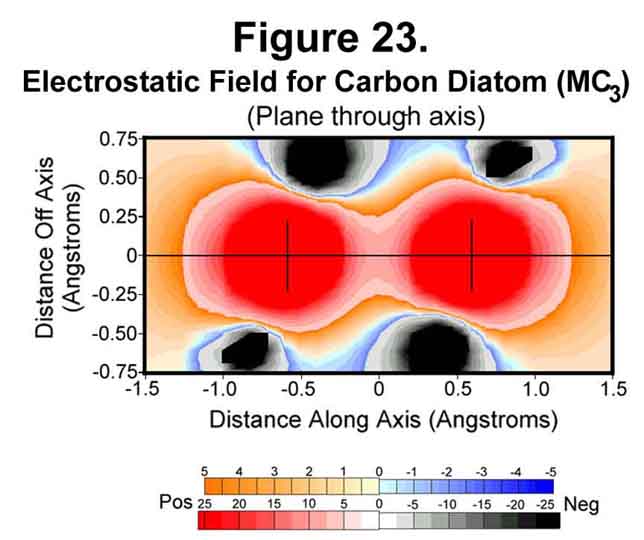
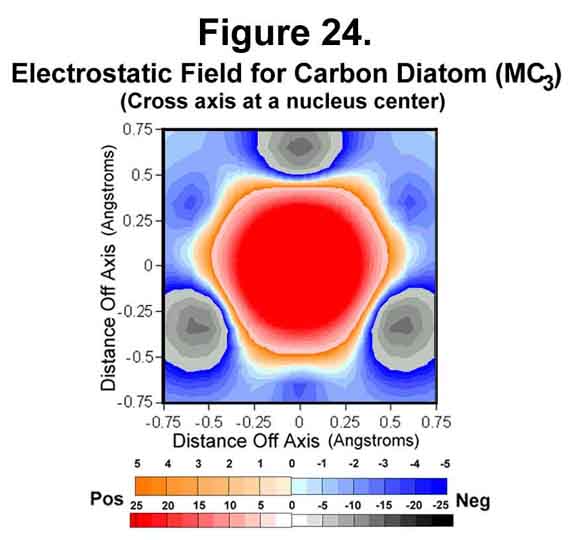
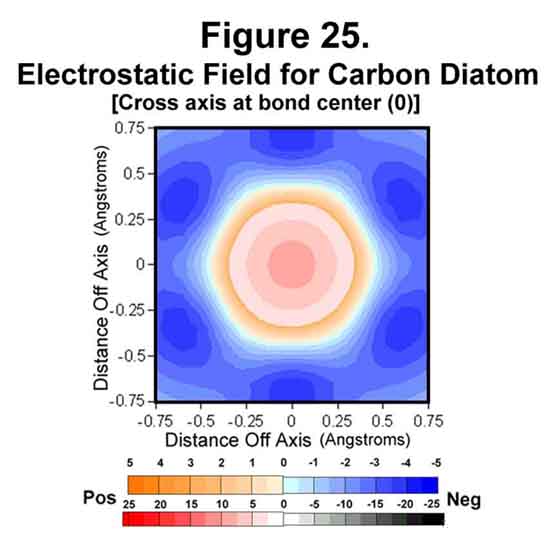
Carbon atoms can join in several ways. In one, the atoms form a "triple" bond. This occurs when two carbon atoms join with M1C3-valence states. Figures 23-25 show the situation for the carbon diatom. The first thing that is obvious is the lack of "negative end-caps". One of the effects of electrons is to channel positive charge. Polymers are thus long, greatly sphinctered threads of positive charge surrounded by negative charge rather than alternating bits of positive and negative matter. Polyacetylene is a rigid "anaconda full of pacas". Because there are anti-Xi electrons, unlike the situation for hydrogen, the cross section through a carbon atom perpendicular to the bond axis has the nucleus well surrounded with negative field (Figure 24). Like the hydrogen molecule, the mid-point of the bond is symmetrical with a strong surrounding negative field (Figure 25).
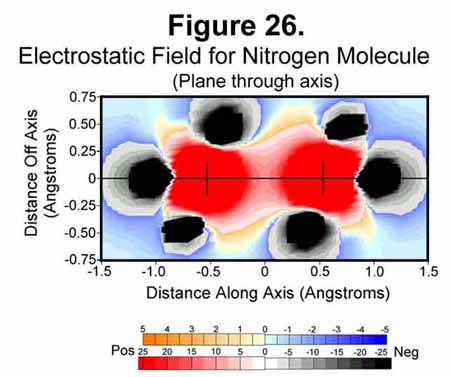
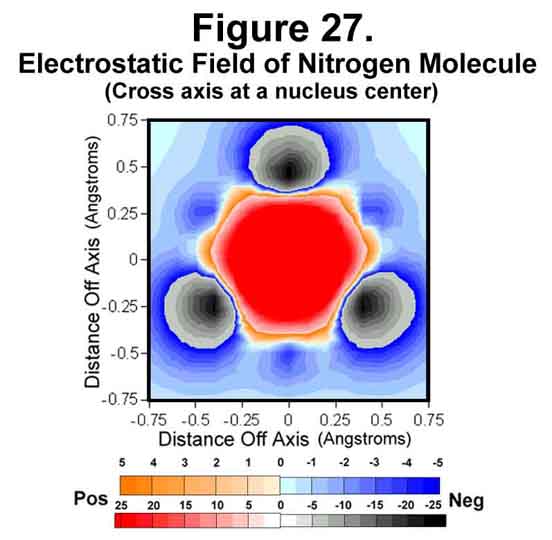
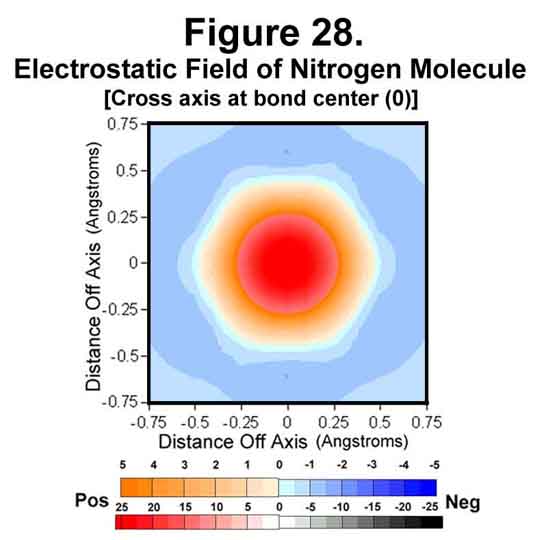
3. NITROGEN MOLECULE
The nitrogen molecule is similar to the carbon diatom except that it has electrons to cover its ends. The electrostatic field around the molecule is shown in Figures 26-28. As can be easily seen, the ends are very well covered and the nitrogen molecule presents a completely negative capsule. The difference of the M (1/4-time) and C (full-time) electrons is easily detected in the field sizes associated with them; especially in the atomic cross-section (Fig 27). As we move to the right in the periodic table, the negative field intensity at mid bond decreases while that around each atom increases.
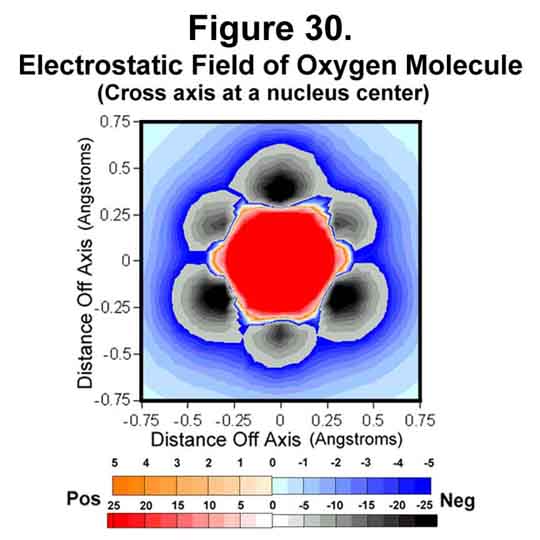
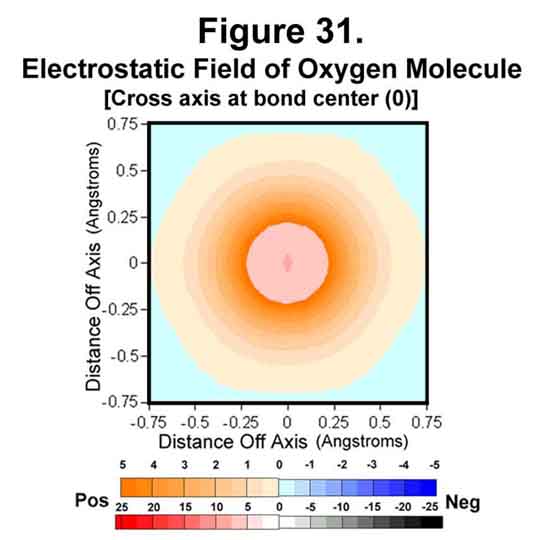
4. OXYGEN MOLECULE
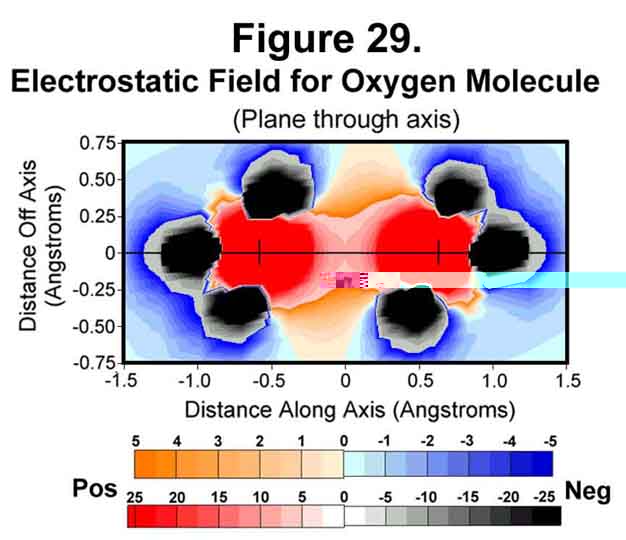
Oxygen is deficient two electrons. In the molecule, 2 electrons fill the three anti-Xi positions of each oxygen atom to accommodate this. This results in a net of two unpaired electrons. The electrostatic field around the oxygen molecule is given in Figures 29-31. The strengthening of field at the nuclei and the weakening at mid-bond continue. The mid-bond is still covered weakly and so the molecule has modest stability among other molecules.
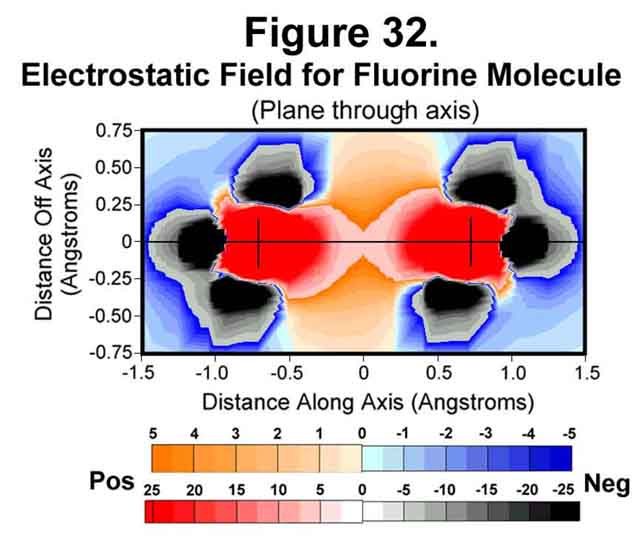
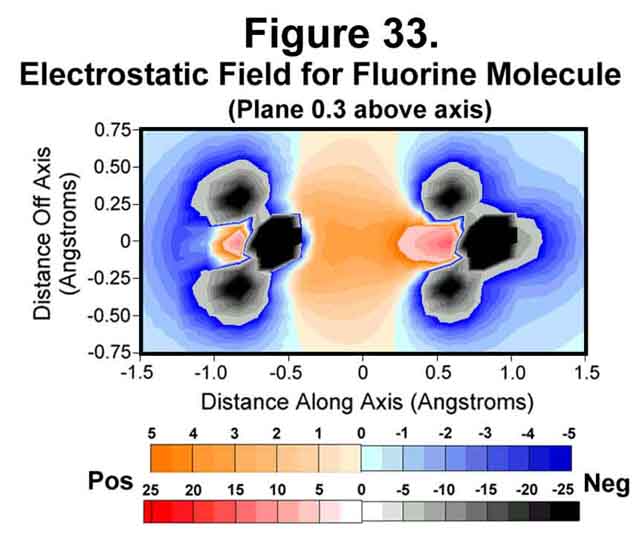
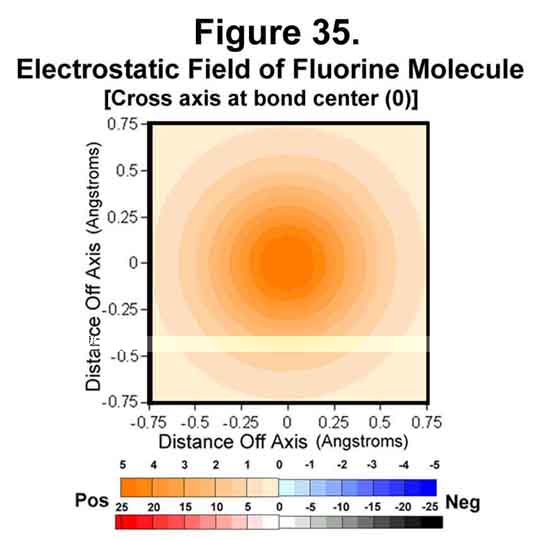
5. FLUORINE MOLECULE
Fluorine is just deficient a single electron. The electrostatic field around the molecule is given in Figures 32-35. The trend of electron concentration around the nuclei and diminishing at mid-bond continues as indicated above. Indeed, while the positive-negative attractions suffice to provide a strong single bond, the mid-bond region is not covered! Thus, fluorine is a more reactive molecule than would be expected from its bond strength.
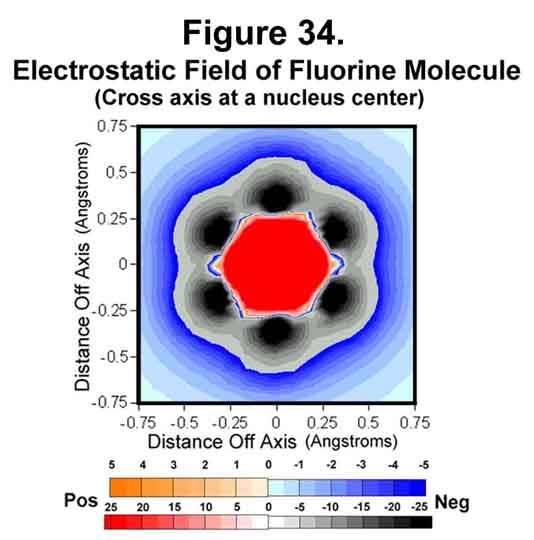
6. NEON ATOM
A cross-section through the neon nucleus would look much like that through the fluorine nucleus (Figure 34), only tighter. There would be no octet deficiency around the neon nucleus, however. Rather, it would be symmetrically well shielded cubically.
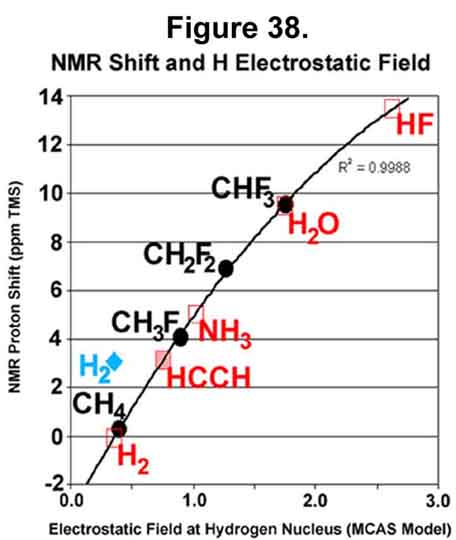
F. PNMR SHIFTS AND FIELD INTENSITY
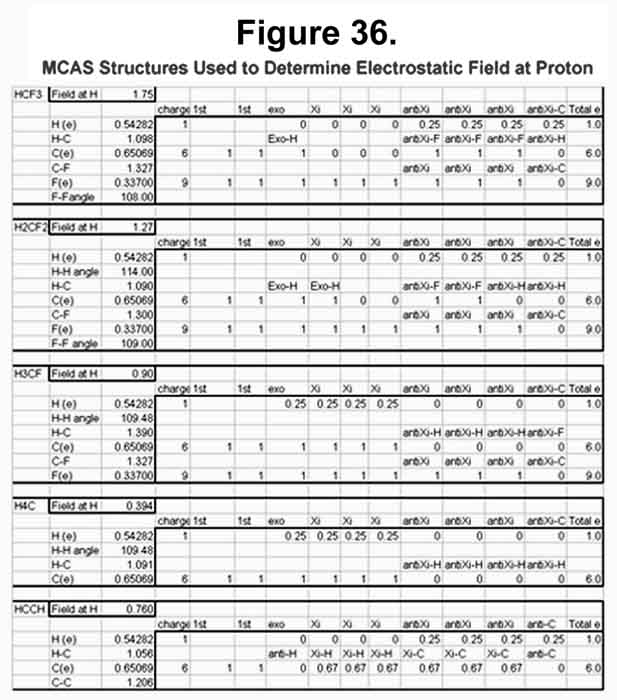
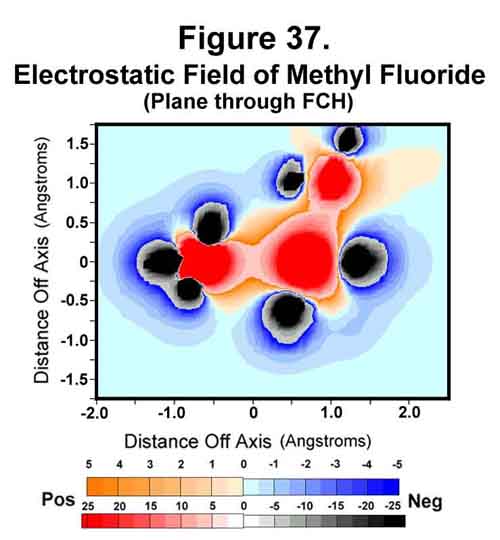
Since the nucleus is essentially a point in the surrounding electrostatic field, the field intensity at its center is a good approximation of what the nucleus will be subjected to. The electrostatic fields of fluoro-substituted methane compounds have been determined and compared to their NMR chemical shifts. In the MCAS system, each hydrogen atom will have a single M-electron. The intensity of this electron and the proton at its center are omitted from the determination, as they are redundant. The MCAS electron distribution and the resulting electrostatic intensity at a proton center are given in Figure 36. Those who want electron density on the axis between two nuclei should find great joy in the difluoro- and trifluoromethane compounds. Note that the carbon electron that would be exo to the C-F bond occupies the "anti-sigma" position. In these, the hydrogen atoms must point one of their lobes towards the carbon nuclei as those "exo" electrons were their carbon Xi-electrons! Indeed, the two hydrogen nuclei in difluoromethane diverge because the two carbon Xi-electrons the two hydrogen nuclei would normally share and, hence, both be attracted to, are gone. Xi-bonding of the hydrogen atoms is favored in methane and fluoromethane. The electrostatic field for fluoromethane is shown as in Figure 37.
Proton chemical shifts of some molecules are compared to the calculated electrostatic fields at the hydrogen nucleus in Figure 38. The fluorinated methane series is shown in black. The NMR shift values are averages of available data [green (From the gNMR freeware program. Information from Neil Glagovich, Central Connecticut State University), purple (From the Central Connecticut State web site: http://www.chemistry.ccsu.edu/glagovich/teaching/472/nmr/factors.html), blue (From the Colby College web site: http://www.colby.edu/chemistry/NMR/H1pred.html)]: methane (0.0, 0.23, and 0.6 ppm relative to TMS), fluoromethane (3.70, 4.26, and 4.1 ppm), difluoromethane (6.86 ppm), and trifluoromethane (9.54 ppm). The relationship appears very good. The red data in the plot for compounds whose location on the fluorinated methane curve is set by their electrostatic data. The data for acetylene corresponds to 3.1 ppm ¾ data is reported [From the Cal State Stanislaus and U of South Maine web sites: http://wwwchem.csustan.edu/Tutorials/NMRTABLE.HTM, http://macweb.acs.usm.maine.edu/chemistry/newton/Chy251_253/Lectures/HNMR/ChemicalShifts.html] from 2 to 3.1 ppm. The data for NH3, H2O, and HF are what would be expected without hydrogen bonding. The HF value is consistent with, and higher than, those of acetic and sulfonic acids [Derome, Andrew E., "Modern NMR Techniques for Chemistry Research", Pergamon Press, Elsevier, Tarrytown, NY, pp32-35 (1987)]. Hydrogen bonding brings a large, negative, electrostatic presence on the exposed side of the proton and can lower the shift value; to <1 for H2O in benzene, for example. Pure water is at 4.63 ppm [Handbook of Chemistry and Physics, 66, F-216 (1986)], which is the midpoint between 9.63 and -0.37 ppm. The electrostatic level for the hydrogen molecule should correspond to a chemical shift just less than that of methane, if the electron around the adjacent hydrogen were always distributed -¼ per tetrahedral lobe. Experimental data [Expected chemical shift, W.T.Raynes, "Specialist Periodic Report NMR", 7, R.J.Abraham, ed (1978) is 26.26 (+/- 0.15) ppm ? courtesy of Nikolay M.Sergeyev, nser@nmr.chem.msu.su. Experimental value of 26.2 ppm given at http://tiger.berkeley.edu/pfrommer/nmr/nmr.html with CH4 (30.61), C2H6 (29.86), C2H2 (29.26), and C2H4 (25.43). These values have been converted by the current author to the TMS scale with a quadratic equation having R2=1.0 for the carbon compounds: CH4 (0.30 set), C2H6 (1.2 set), C2H2 (1.8), C2H4 (4.7 set), and H2 (4.1)] ? this web site is no longer available], however, place the chemical shift of the hydrogen molecule proton near that of ethylene! The blue location for the hydrogen molecule represents the electrostatic field at the proton when the electron of the adjacent hydrogen is in the lobe exo to the bond. Momentary presence appears more important here than time-averaged probability.
G. SUMMARY
Single bonds between atoms do not
need paired-electron couplets on the axis between the two atoms.
Bonding can be satisfactorily explained by minimizing inter-atom
electron-electron and proton-proton repulsions, while maximizing
inter-atom proton-electron attractions of non-axial components.
Opposing electron motion (alignment with or against the field) rather
than spin-reversal provides spin-pairing. Triple bonds are just single
bonds with less inter-atom electron repulsion. The anti-bonding orbital
is in the axis of the bond, not opposite it. Under proper conditions,
one electron can fill this anti-bonding orbital in a stable molecule.
Classical electrostatic calculations and the MCAS approach provide a
satisfactory explanation to atomic covalent bonding without the need
for waiving the electron-electron repulsion necessary to generate high
negative density in current approaches. The MCAS approach to the
electronic structure of atoms and their interactions allows ionic and
covalent bonding to be explained by the same set of rules.
PART III

A. INTRODUCTION
The overlap integral of molecular bond making is discussed first. Atomic orbital orthogonality is treated by the same approach. This discussion is followed by the designation of new quantum numbers for the orbitals of atoms described by the MCAS way. Electrons occupy these orbitals, but have no numbers themselves.
B. ONE ELECTRON PER ORBITAL - PAULI
Density functions are electrostatic field intensities associated with the probabilities of a particulate electron actually being present. No problem when only 1 electron is present. When two regions are overlapped to yield atomic or molecular orbitals, the resulting particulate probabilities in the overlap are determined in the current QT as cross-products and new field intensities related. The cross-product in the Schrödinger equation must be for an electron and it can not be an instantaneous sum of two electrons ¾ probabilities may by fractional, but orthogonal particles are not. If cAcA [read A OR A, not A AND A] and cB2 [read B OR B] correspond to 1 electron each, then so do cAcB [read A OR B] and cBcA [read B OR A]. Since the last two refer to the same region, the sum must be (A-NOT-B + B-NOT-A) or (A AND B). The last (used in the current QT) defies electrostatic law. One component or the other of such an overlap (if it could exist) would also repel the non-overlapped region at the interface. These are not bank mergers. The first summing can occur only when the regions oscillate reciprocally into the overlap.
Consider two single point, atomic orbitals leading to a molecular orbital. This extreme case starts with two incompatible, electrons at two, separated, infinitesimally small points ¾ each point, thus, has a probability of 1. Each electron has an identical, but separate nucleus. If the two points are combined, the combined point can also have a probability of 1 with respect to an electron. Thus, the overlap point can have an entity present; one, not two ¾ electrostatic orthogonality (repulsion) forbids the combination of the two electrons into a single entity. The entity combination is OR not AND. That other entity must be put elsewhere. In other words, there must be a second location with a probability of 1 after overlapping. If neither electron occupies the overlap point, then there must be two other locations. The algebra goes
YAB2 = (cAj A + cBj B)2 = cA2j A2 + 2cAcBj Aj B + cB2j B2 ……………………………………… (1)
For this point orbital case, cA = cB and j B = -j A (opposed orbitals equally placed between the two identical nuclei). Thus,
YAB2 = pA - 2pAB + pB = 0 (The overlap is a node!)……………………………………………… (2)
pAB = 1. ………….…………………………………………………………………… ………………… (3)
Taken further, as soon as one infinitesimal point is assigned the probability of an electron being present, points an infinitesimal distance away must also be assigned that same electron. Carrying this to the overlap boundary converts the OR-sum to an A-NOT-B or a B-NOT-A sum. Thus, an overlap region can possess only A-OR-B, but not both at the same time. In essence, renormalizing resets the total probability to unity for an electron. The result of this is that when two regions (orbitals) overlap, they must overlap completely, not partially, with respect to an electron being present. An electron, if present, may have a very low probability of being in the far parts of the overlap, but that finite probability precludes another electron from being in the overlap. If the total electrostatic field in the overlap is greater than the contribution from one electron within the overlapped region, the additional contribution must come from without. If the overlap field is less than that from one electron, there can be no full-time electron in the overlap. Indeed, there may never need to be an electron in the overlap. All electrostatic density might come from without. There must, however, be unoccupied orbital space (probability always able to be 1 as that is what defines orbital space) available elsewhere for any excess electrons that were in the orbitals that were overlapped!
Atomic orbitals conform to a similar treatment. j A is the pA® eA single point, orbital vector for electron A and its associated nucleus A. The complete atomic orbital for electron A is the vector space in which the pA end of all the vectors is the same point. The reverse of the vector is -j A (eA® pA)! Molecular orbitals are formed by "noding" the negative (electron) end of proton-electron vectors. Atomic orbitals are formed by "noding" the positive (nucleus) end of these vectors. Equations 1-3 above hold for both. In the case of the atomic orbitals, protons A and B are overlapped between the two electrons. When the overlap demands A-OR-B, there is no problem as A and B are one and the same. The three nodes have a particle each ¾ nothing extra. For the nucleus to remain a node, the two electrons must act as a synchronous, opposed couplet. The simplest (a guiding scientific truism) orbital structure that can be generated in spherical space without the two electrons occupying the other's space is one of diametrically opposed tetrahedra. Particle spatial probability may be random over time, but it is highly unlikely that this couplet moves randomly!
The "miracle" of the spdf-based quantum theory arises from allowing the renormalized probability summation of the overlapped and unlapped regions to represent 2 electrons and waiving the particle exclusion (repulsion) aspect of the exclusion principle. Pauli originally had no more than one electron per box ¾ his requirement that each electron have a separate identity. [The exclusion principle simply reiterates the axiom that no two objects can occupy the same space at the same time!] Actually, it is the quantum box that has the number, not the electron which may or may not be present. When two boxes are overlapped, a single box with [A OR B OR neither] should result, not three pseudo-boxes with {[(1-fA)A] + [(fAA+fBB)] + [(1-fB)B]} or one box with [A AND B]. Overlapping two boxes allows the system to reduce its electronic deficiencies, allows one electron to serve the purpose of two, and/or frees an electron for more constructive use elsewhere! The energy change can certainly be related to the hypothetical overlap integral that would result if electrons were combinable, but that does not verify that such an overlap actually occurs! Treating orthogonal electrons like money is what allows the current QT to subtly sell "two e's in a pod".
The single point orbital is the very center of the current Quantum Theory's overlap between two identical atoms. It should be the point with the highest probability of electron presence, yet Y 2 = 0 ¾ even when an electron is present! Does ò Y2dr = 1 with two electrons present flow logically from this?
C. MCAS QUANTUM NUMBERS
Quantum electronic levels are energy levels that correspond to discrete synchronous actions and interactions of electrons among themselves and with their nucleus (or nuclei). Precise interactions (energies) are required to be "in-synch" while moving at nearly the speed of light. Orbitals define where the electrons of these synchronous actions and interactions physically reside. The probability description (negativeness contour) of the orbital will correspond to the time-averaged electrostatic radiance of an electron when present. Since orbitals form sets and subsets, discrete identities (quantum numbers) can be assigned to them. The electrons that occupy them do not have quantum numbers! An electron may enter an orbital as another is leaving, but two electrons can not harmoniously occupy the same orbital space at the same time ¾ a requisite of orbital space (electrostatic particle orthogonality). Since several orbitals may form a group, electrons can synchronously visit separate orbitals of the group. Taking a time interval from mid-occupancy to mid-occupancy to indicate that two electrons can share the same orbital at the same time would be statistical quackery. Electrostatic field additivity cloaks electrostatic particle orthogonality. Probability might not know the difference, but electrons do.
The Pauli exclusion principle is about energy "boxes" (orbitals, levels). Orbitals exist from a quantum number aspect whether they have an electron in them or not. That is, they represent allowable synchronous interactions. The orbital "spin" factor corresponds to an orthogonal set of diametrically opposed, non-coincident orbitals. This factor should have been called the "ort" factor instead of the "spin" factor. An electron does not set the orthogonality of an orbital. Rather, electron spin allows the electron to shape the orbital terrain. E.g., 100(+½) H Street and 100(-½) H Street are contoured as mirror images. The combined lot relinquishes the orthogonality component to become 100(0) H Street. It still must obey the single occupancy zoning law (electrostatic particle orthogonality), however. Since an electron need not be present at all, ever-present orbital "spin" ("ort") is unrelated to the spin of an occasionally present electron!
Each atomic orbital has a unique quantum number (currently specified by nlms, although nlmo would have been better as it would have severed the implied connection to electron spin) that permits instantaneous, harmonious, space assignment to an electron. For the MCAS approach, "stogh" (pronounced "stow", where s = shell, t = type, o = ort, g = group, and h = ‘home’ orbital) is used in place of nlms. Shell has a value 1-n; type is 1-4 (M=1, C=2, A=3, S=4); and ort is +1 or –1 (mirror-image type sets). The number of groups in each orbital type is: 1 for M; 2 for C; 3 for the transition (A orbitals) series; and 4 for the rare earth or actinide (S orbitals) series. The ‘home’ orbital value specifies the group lob. The M-orbital type has a single group that has 4 orbitals. For the M-type, the same electron occupies all four orbitals and h can only be 1. For the C-orbital set, h is 1-2. For the A-orbitals, h = 1-3, while h = 1-4 for the S-orbitals (see below).
For the H atom, the ground state electron is in the 11111 orbital [as opposed to the nlms 100(+½)]. The first electron in He is the same, while the second is in the reciprocal set.
|
|
1st e |
2nd e |
|
H |
11111 |
|
|
He |
11111 |
11-111 |
The orbitals for the 3rd to last Aufbau
electrons in the ground states of the second row elements are
|
|
3rd e |
4th e |
5th e |
6th e |
7th e |
8th e |
9th e |
10th e |
|
Li |
21111 |
|
|
|
|
|
|
|
|
Be |
21111 |
21-111 |
|
|
|
|
|
|
|
B |
21111 |
22-111 |
22-112 |
|
|
|
|
|
|
C |
21111 |
22-111 |
22-112 |
22-121 |
|
|
|
|
|
N |
21111 |
22-111 |
22-112 |
22-121 |
22-122 |
|
|
|
|
O |
22111 |
22-111 |
22-112 |
22-121 |
22-122 |
22112 |
|
|
|
F |
22111 |
22-111 |
22-112 |
22-121 |
22-122 |
22112 |
22121 |
|
|
Ne |
22111 |
22-111 |
22-112 |
22-121 |
22-122 |
22112 |
22121 |
22122 |
"stogh" designations allow each orbital space to be specified. Whether electrons move into and out of orbital groups or not, they must have a unique ‘home’ orbital. Changes in the underlying electronic structure may occur as additional electrons are added. These changes are accompanied by the appropriate change in the "stogh" designation. The changes in the type designation of the 3rd and 4th electrons above, for example, reflect additional electron loading in the M-orbitals to convert them to C-orbitals. Converting the –1 "ort" set to higher loading first is a matter of convention as the third and fourth electrons are identical. When there is no external field, 22-112 and 22-121 are equivalent and filling of either can occur before the other. In the presence of a field, however, the lowest energy state fills first. Quantum numbers are easily related to the field by placing the x-y-z axes through the MCAS cube faces. Note the primary alignment to the field running - - - to +++ and secondary ones along the axes.
For A-orbitals, there are two opposing sets of nine subdivided into three sets of three (coplanar) ¾ g = 1-3 and h = 1-3 (one orbital is face-centered and the other two are edge-centered in the MCAS approach). For S-orbitals, there are two opposing sets of sixteen subdivided into four sets of four [a "C" set rotated 60º (relative to the standard C-orbital) about the "corner" orbital] ¾ g = 1-4 and h = 1-4 (one orbital is corner-directed and the other three are squared-faced in the MCAS approach). The theorist can add, subtract, multiply, or do whatever (even change) these numbers to allow him/her to "integer-ize" his/her mathematics. (+½ and -½ must be integer quotients in the nlms scheme!) Indeed, the theorist might find it convenient to consider the C orbital as just a more heavily loaded M-orbital (or vice versa) since there are no new orbital spaces defined. From a pragmatic point it seems desirable to separate them to emphasize the uniqueness of the single loading of multiple orbitals. The numerical symmetry, as demonstrated below with the inert gases, is quite suggestive, too! 2s2 gives the maximum number of electrons (2, 8, 18, 32) in the s-shell!
|
Shell |
Element |
Electrons |
MCAS Structure |
stogh of last electron in shell |
|||||||||
|
|
|
|
|
1st |
2nd |
3rd |
4th |
5th |
6th |
||||
|
1 |
He |
2 |
M2 |
11-111 |
|
|
|
|
|
||||
|
2 |
Ne |
10 |
M2C8 |
11-111 |
22122 |
|
|
|
|
||||
|
3 |
Ar |
18 |
M2C8C8 |
11-111 |
22122 |
32-122 |
|
|
|
||||
|
4 |
Kr |
36 |
M2C8A18C8 |
11-111 |
22122 |
33-133 |
42122 |
|
|
||||
|
5 |
Xe |
54 |
M2C8A18A18C8 |
11-111 |
22122 |
33-133 |
43133 |
52-122 |
|
||||
|
6 |
Rn |
86 |
M2C8A18S32A18C8 |
11-111 |
22122 |
33-133 |
44144 |
53-133 |
62122 |
||||
The "ort" values will be determined by the field relationship chosen to define the orbitals. The sequence is alternated here, although the "last" electron in each shell should be against the field. The conversion of the 5th shell C-orbital system to an A-orbital set with one electron to allow the conversion of the 4th shell A-orbital set to an S-orbital set is the main factor why the primary valence of the lanthanide series is +3 (J.M. Williams, "The Electronic Puzzle, US LibCong ©1994).
No electron has a quantum (plat) number ¾ only an orbital! Every electron must have a ‘home’ address, however. The "miracle" of the current Quantum Theory occurred when two opposing orbitals were allowed to merge into a sphere (Bohr's orb ¾ Pauli's mentor) and their "spin" ("ort") numbers, which defined immobile physical space (as diffuse and probable as required), transferred to two electrostatically antagonistic, mobile electrons. Mathematical magic.
D. NO NEED FOR PARTICLE THEORIES?
The challenge for any QT is to include particulate solutions that satisfy electrostatic requirements, if they are to claim completeness and robustness and, of course, to be correct. The MCAS particulate model gives electrostatic solutions with all e-e repulsions "orthogonalized"; i.e., e-e overlaps are minimized. These solutions are excluded from the currently accepted QT, however, where maximized e-e overlap is the rule!
The reason MCAS solutions are excluded from the current QT is the special attribute given to electron spin-reversal in this QT. Spin-reversal is a form of orthogonality. Unlike orthogonality practiced elsewhere in the current QT, however, spin-reversal orthogonality negates e-e repulsion rather than "orthogonalize" it!
The MCAS approach will raise the ire of those who have bought spin-reversal bonds. The ultimate QT must be reconciled to ALL aspects (probability, wave, AND particulate). As the particle component apparently sets a stricter bound than probability, the appropriate response is,
"If you want a theory that is correct, you need to address particulates, too".
PART IV

A. MODELS and REACTION PATHS
Before proceeding, it is appropriate to comment on: some MCAS structures (hydrogen, carbon, and the halogens) and microscopic reversibility.
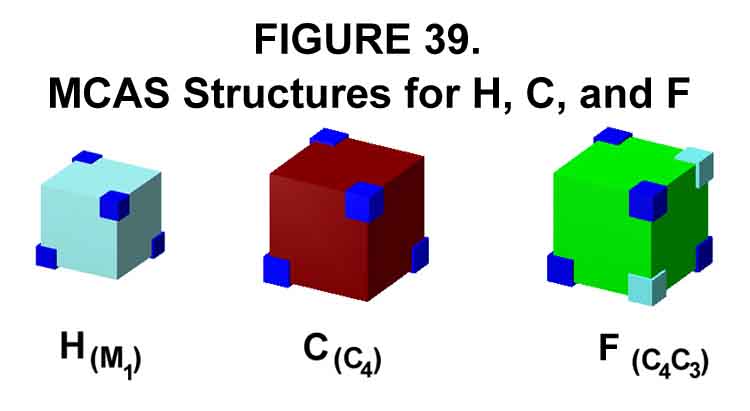
1. MCAS MODELS OF SEVERAL ATOMS
The MCAS structures for hydrogen, carbon, and fluorine are shown in Figure 39. The blue and aquo corners indicate the directions of orbital lobes. Note the two sets. Hydrogen is in its M1M0 base state wherein one electron roams a mono orbital occupying tetrahedral space. Carbon is in its C4C0 (four orbitals tetrahedrally oriented in cubic space) elevated state needed for four singles bonds, rather than its M1C3 (M and C's counterpoised) base state. Fluorine is in its C4C3 (two C units counterpoised) base state. The MCAS structures are nicely understood with the use of cubes. Every electron in the MCAS methodology has its own instantaneous orbital space. Electron pairing occurs through diametrically opposing motion rather than through spin-pairing and negative-negative repulsion negation required for dual orbital occupation.
2. MCAS versus Currently-Accepted MODEL OF METHYL FLUORIDE
Models for methyl fluoride are shown in Figure 40. Like the MCAS cube model for carbon, a cube representation for carbon in the currently accepted vernacular nicely depicts the spatial orientation of the orbitals (sp3) - larger dark blue corners indicate 2 electrons per lob instead of 1. Think spheres for the cubic hydrogen atoms in the currently accepted model, however. Like carbon, the cube represents fluorine well whether it is the currently accepted (sp3) or MCAS model. Other halogens will be larger than fluorine. The important feature is their common C4C3 outer shell, however. Cubes are use for the currently accepted model to help with spatial effects and because spheres and tetrahedral shapes are not available with the modeling program used.
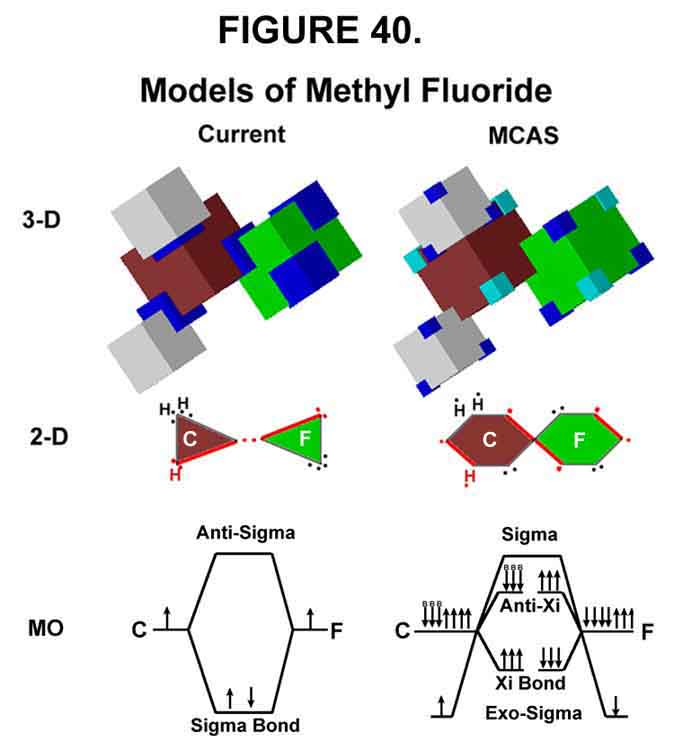
The 2-D models shown in Figure 40 give a touch of 3-D character to the planar. The dense red lines indicate point-to-point lines in the plane of the paper. Two H's or two electrons at any point in the MCAS representation should be interpreted as one above and one below the plane. Wedges would give even more 3-D character. In the currently accepted representation, one H and two electrons are above and one H and two electrons are below, while four electrons should be read two up and two down. The similarity between this 2-D representation of the currently accepted model and the Lewis octet structures should be apparent. The more dispersed electron nature of the MCAS structures should also be obvious. Every electron in the MCAS methodology has its own instantaneous orbital space. Electron pairing in the MCAS models occurs with opposing motion rather than orbital overlap, however! Negation of negative-negative repulsion (required for two electrons to be in the same orbital) is not needed in the MCAS methodology as it is in the currently accepted methodology. Thus, in the MCAS models, the sigma bonds have no electrons in them. The bond between the carbon and the fluorine is called a sigma-Xi (sX) bond; as are those between carbon and hydrogen.
The MO for the currently accepted methodology is straightforward, IF spin-paired negation of negative-negative repulsion is accepted. The MCAS MO depicts the bond between the carbon and fluorine as a 6-electron Xi bond (see the 3-D view for the electron placements). The three electrons on the opposite side of the fluorine and the three CH bonds (B-arrows) oppose the Xi bond. The Xi/anti-Xi levels are shown with no net change in energy, although this is not the case. The net gain in energy in forming the bond is allotted to the exo-sigma electrons that are now paired by opposing action. They are placed on opposite sides of the atoms from the bond to give them spatial meaning. As noted before there are no electrons in the sigma bond ¾ only overlapped negative fields. Placing electrons in the bond negates the reason for forming the sigma bond.
3. MICROSCOPIC REVERSABILITY IS NOT
Microscopic reversibility has been invoked to justify that SN2 racemization reactions have a single Transition State regardless of direction. The rationale being that momentum (and every other action!) is instantaneously reversible at every moment. This seems a rather unlikely situation for this type reaction! Indeed, the situation is much like pole vaulting. The vaulter starts down the runway and vaults up but not over. Eventually, he vaults over the wall feet first. After falling down on the other side, the vaulter goes to the head of the runway and reverses the event - again feet first over the wall. In the macrosense, the forward and reverse actions are identical, although the attempts might not be the same! At the instance of going over the wall, "the Transition States" of the two are mirror images! The fall after the max is the same for the forward and reverse; neither the same as the rise - to imply otherwise, as is commonly done, over simplifies and misleads. In the more correct and, I believe, original interpretation of microscopic reversibility with Y1 and Y2 identical (!),
Y1 + RY2 ® Y1R + Y2 and Y1R + Y2 ® Y1 + RY2
proceed through identical paths. Since, in this case, the forward and reverse reaction paths are mirror images, the Transition States will be mirror images. Having the two Transition States be independent of path direction (centrosymmetric here) would be most unusual, but still highly touted! The pre-transition and post-transition routes might, however, be similar as in the graphical presentation of Figure 41.
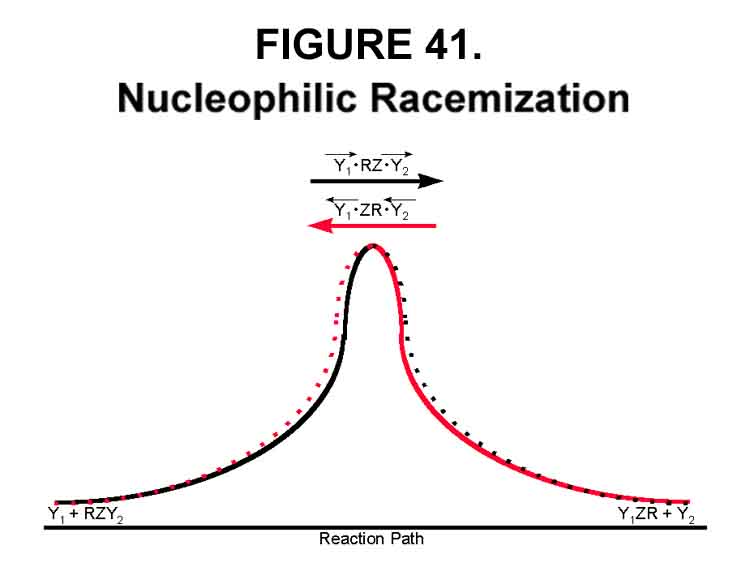
The Transition State is said to be the highest energy level to which reactants can go, reverse momentum, and return to base. In this sense, an infinite summation of momentum reversals equates to microscopic reversibility. No single trip up the energy curve, however, is reversible at every point - only at its energy maximum! Only the maximum-maximum Transition State can reverse in either direction and then only if it is path-independently identical. More generally, the Transition State is that assemblage on the reaction energy path at which the assemblage components can NO LONGER reverse to base.
B. SN2 REACTIONS THE MCAS WAY
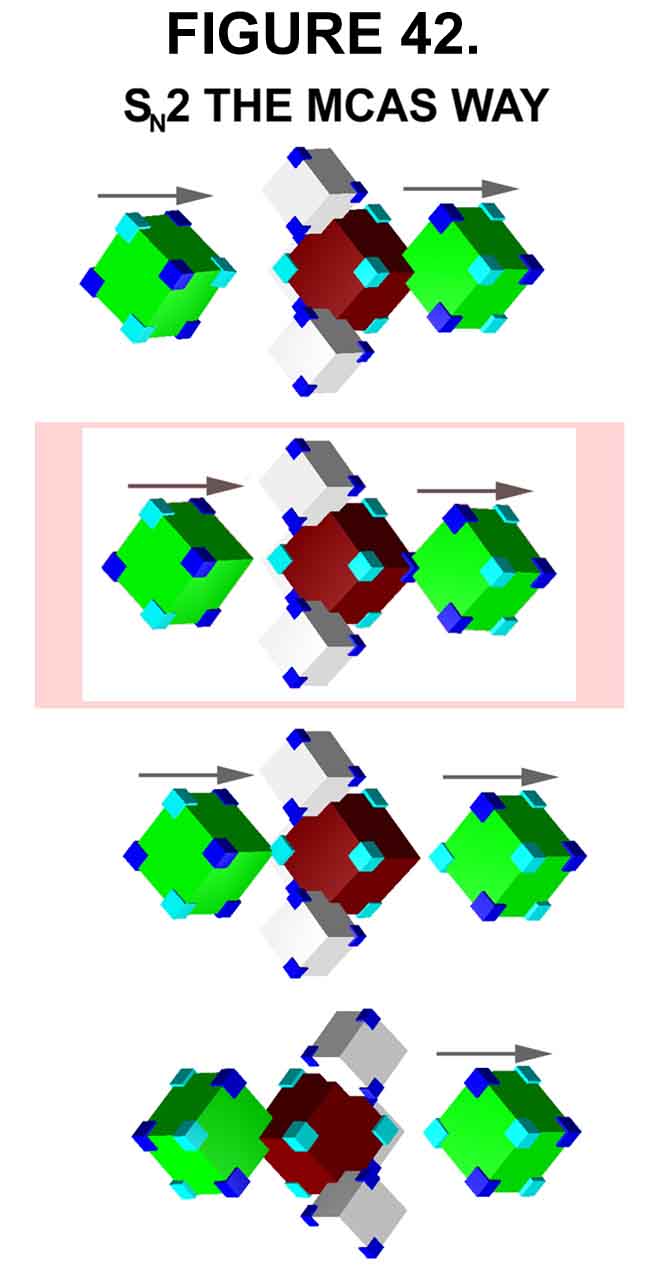
The C¾ Y2 bond is constantly stretching and contracting. When the bond stretches extensively, the exo-sigma electron (low-energy state - carbon in C4C0 state) moves to the sigma bond (high-energy state - carbon now in a C3C1 state) to minimize charge separation (see the MO in Figure 40). [Note that when ·CF· becomes C·F·, it becomes naturally highly polarized (+ - + -)!] Stretching becomes more difficult as bond energy increases - thus, a strong dependence of leaving group propensity on bond energy. If the stretch is violent enough, the Y2 group will leave with the electron in spite of the separation of charge ¾ SN1 type. Usually, however, the C¾ Y2 bond returns to normalcy and the electron returns to the exo-sigma orbital (C3C1 returns to C4C0 ¾ MCAS vernacular). If there is an e-donor (Y1) nearby when the exo-electron is transferred to the sigma bond, this e-donor can supply an electron to the now vacant exo-sigma orbital, IF the electrostatics (electrode potential) is satisfactory. When this occurs, the electron in the sigma bond can no longer return to the exo-sigma orbital as the carbon is in the C4C1 state. The destabilized sigma bond now dissociates with the Y2 group leaving with the sigma bond electron. This allows the bond to dissociate at significantly lower Transition State energy as charge separation is minimized. The e-donor, now electron deficient, follows its electron and, thus, "attacks" the carbon. At this point, the C3C1 carbon reorders to C0C4, the non-dissociating bonds on the carbon move to their new location (Walden inversion), the leaving group is further repelled, and the "attacking" group forms a sigma-Xi bond with the carbon. The sequence is depicted in Figure 42, where the e-transfer step (the Transition State) is highlighted.
Carbon will become more positive in the Transition State as the leaving group stretches away. Therefore, electron-withdrawing groups on benzyl halide should retard the reaction by making carbon C4C0 to C3C1 more difficult. The reaction of pyridine with substituted benzyl bromides in acetone shows just an effect [Sudgen, S. and Willis, J.B, J. Chem. Soc., 1460 (1951); cited in Physical Organic Chemistry, J. Hine, McGraw-Hill, New York, p172 (1962) with an earlier reference to Baker, J.W. and Nathan, W.S., J. Chem. Soc., 236 (1936).].
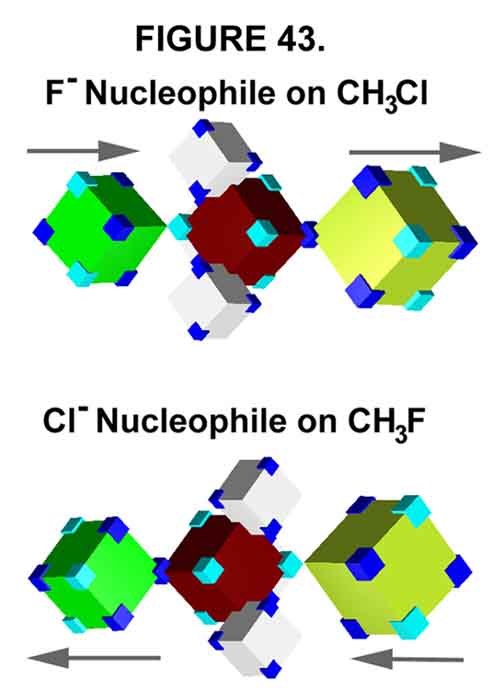
The Transition States of F¯ + H3CCl and FCH3 + Cl¯ are shown in Figure 43. Note that the two do not have the same Transition State (hence, identical energy levels are not required). At the time of electron transfer ("the kicker"), the two are neither superimposable nor mirror images! The same Transition State exists only IF all the atoms (and electrons for that matter) are in identical positions; i.e., they must be superimposable. In the currently accepted explanation of SN2 reactions, the amount of bond formation and bond breaking are said to differ (polarization invoked to explain the halogen behavior, see below). A superimposable Transition State exists only if attacking and leaving groups are identical; maybe not then ¾ just mirror images! Microscopic reversibility, in this sense, is trashed.
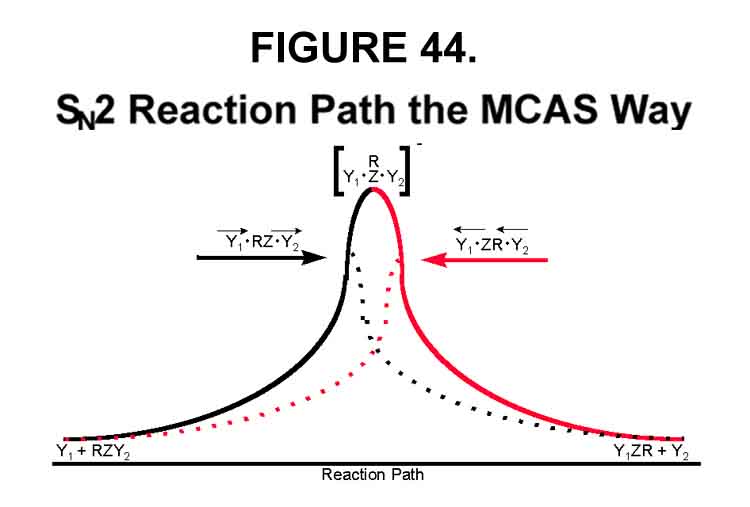
One way to think about the SN2 reaction is to consider the barrier as a moveable incline. The lowest energy path available without help is the top of the incline (actually a saddle in energy space) at its highest level. When this occurs, the Transition State is path-independent (centrosymmetric when Y1=Y2) and should be governed by bond strengths. The nucleophilic center and its associated groups (all those R's) will be in their maximum energy (planar) state, however - maximum-maximum! At the moment this transition forms, all components are stationary. Indeed, microscopic reversibility is possible (see Figure 44). If the height of the incline is suddenly lowered while the species are racing up it, however, they will careen over the brink and down to the base on the other side. In the MCAS version of the SN2 reaction, electron transfer suddenly lowers the height of the incline. The lowering need not be, and is very unlikely to be, the same in both directions. Note that when Y1=Y2, Figure 44 becomes Figure 41 if the upper portion between the two Transition States is eliminated. The Transition State is direction dependent and not reversible, however! A microscopic reversal in atomic positions is hardly sufficient to allow the electron to overcome the energy barrier required for its return. Thus, a microscopically reversible Transition State becomes a very rare event ¾ the most energetic way to go.
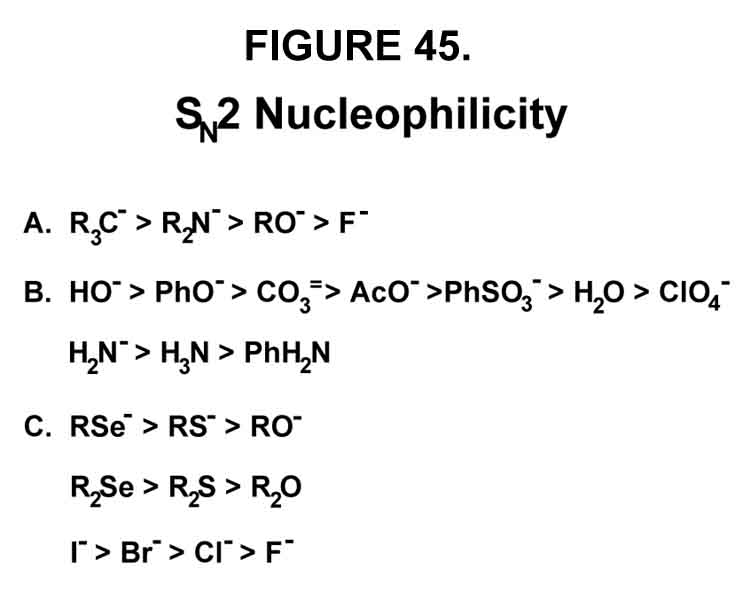
e-Transfer is "the kicker" that destabilizes the bond of the leaving group (Y2) at a time when Y2 has moved away (stationary or no) from the carbon atom and, thus, facilitates SN2 substitution. It is called "the kicker" because, even if the leaving group has stopped moving away (the situation when the molecule has just enough energy to reach this point), it gives it a "kick". The nucleophilicity of some species are given in Figure 45 [Gould, E.S., Mechanism and Structure in Organic Chemistry, Holt, New York, 259, (1959)]. Those in series A and B have the same nucleophilicity order as their basicity or bond strength. In the currently accepted scheme, strong bonds make for strong initiation. Those in series C have the reverse relationship ¾ polarization invoked to explain the turn-about. Of course, polarization is mainly the ability to "depart" with one's electrons. All three series should, however, correlate with the following, 1-electron transfer, half-reaction: RZ· ¯¯ ® RZ + e¯
In 1954, Edwards [Edwards, J.O., J. Am. Chem. Soc., 76, 1540 (1954); O. Foss, cited therein, is credited in 1947-1949 with observing that nucleophilicity followed electrode potential. Edwards showed it was mathematically the dominant factor!] demonstrated mathematically that the oxidation potential of nucleophiles was the dominant factor in their nucleophilicity. The exact reason unclear until now.
C. ELECTROSTATICS OF METHYL FLUORIDE
Electrostatic models of methyl fluoride support the SN2 reaction model given above. Fluoromethane is a simple molecule with an electronegative leaving group. Fluorine is not a particularly good leaving group, because of its strong bond with carbon, but it provides the necessary ingredients for illustrating a SN2 reaction. Figures 46-48 show the permanent polarization afforded by the fluorine atom attached to methane and the extreme polarization effected by the transfer of the exo electron to the C-F sigma bond. Note the repulsive interactions in Fig 48 created when there is an electron in the sigma bond!
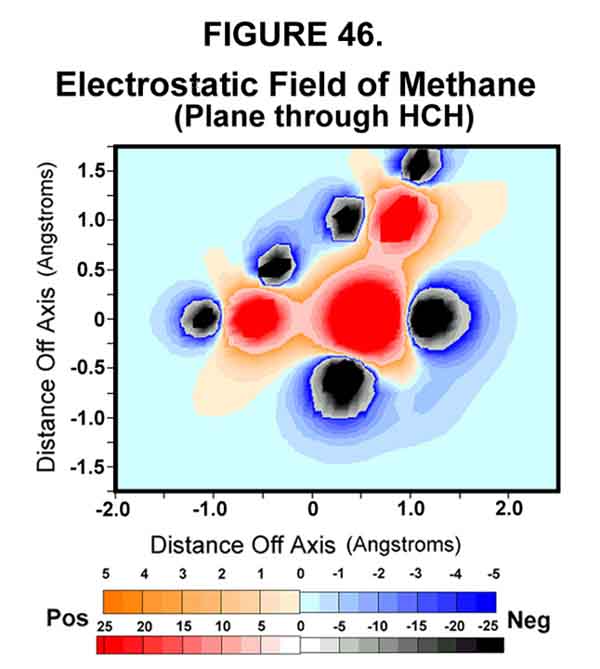
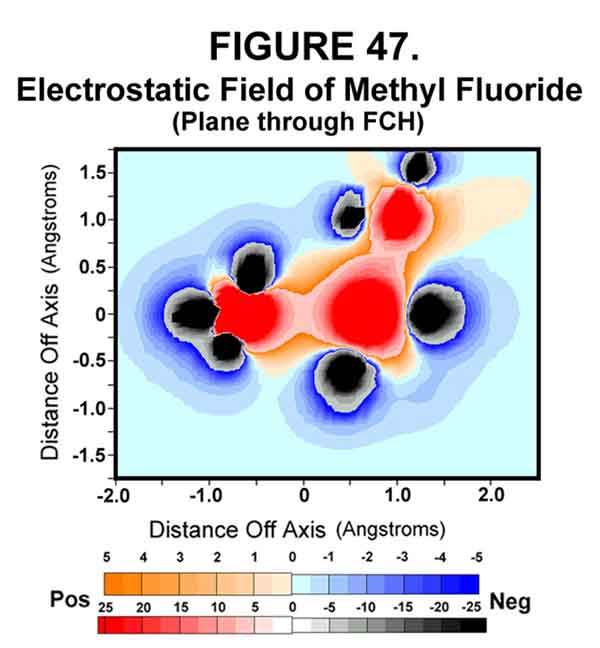
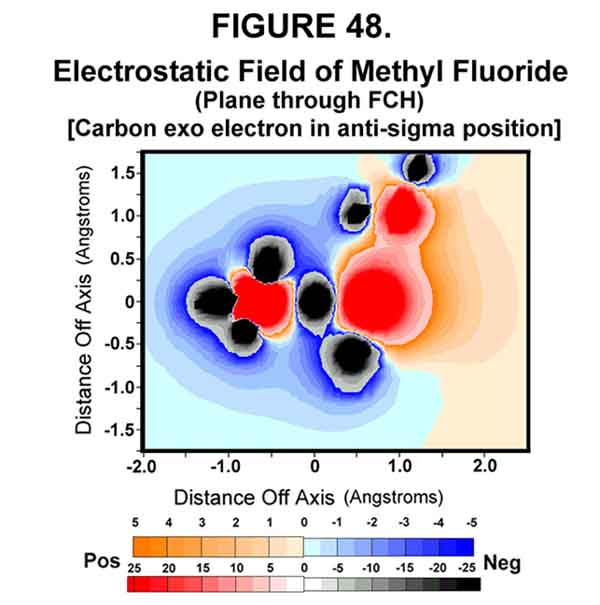
Figure 49 shows the negative repulsions that result when an electron is transferred to the molecule during the transition state.
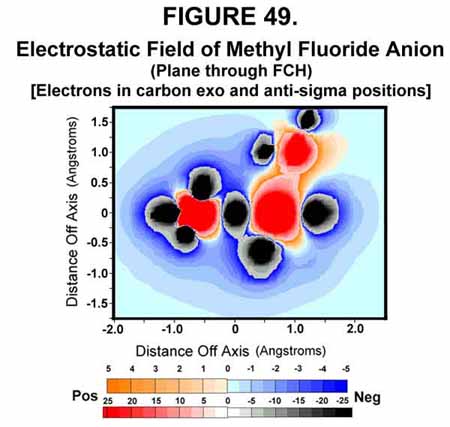
Figures 50 and 51 show the electrostatics opposite the sigma bond before and after the exo electron is transferred to the sigma bond. As seen, the exo electron protects the carbon from attack opposite the bond.
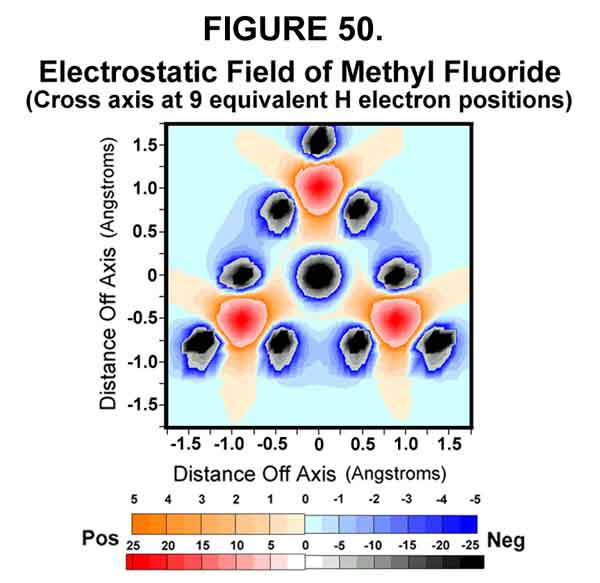
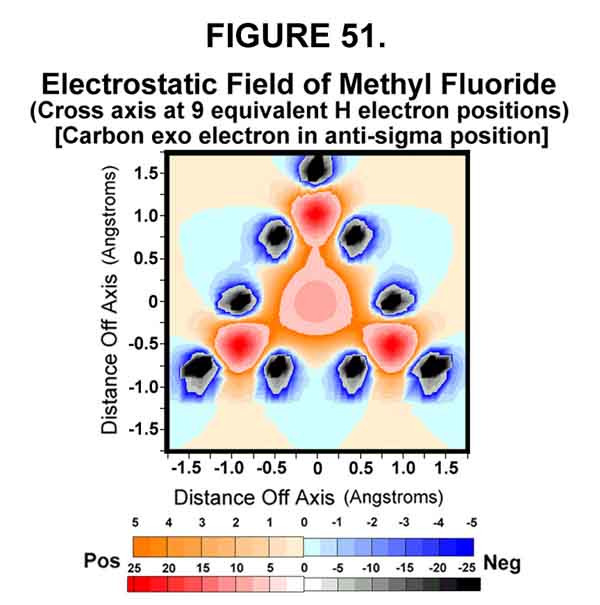
The previously protected posterior of the carbon now provides a rather strong "attraction" for "loosely attached" electrons (Figure 51). If none is around, the electron will shift back to the exo-position, as the carbon-end of the bond is now more electronegative (positive) than the fluorine-end. Actually, the electron is still part of the carbon's orbital system. If, however, an electron jumps from the protruding lobe of a nearby donor (irreversible REDOX lightning!), the fluoromethane molecule becomes an anion and the anti-bonding electron can no longer return to the exo-position, but departs with the fluorine atom (Figures 42 and 49). "Push" is provided by the repulsion between the anti-bonding electron and the three carbon electrons that formed the C-F sigma-Xi bond. As the leaving group departs, the nucleophile that lost the electron follows that electron to form a new, sigma-Xi bond with the carbon atom. The carbon electron structure and the accompanying substituents undergo Walden inversion.
D. SUMMARY
There are no electrons in the sigma bond in the MCAS methodology. Those corresponding to the bond are exo (on the other side of the atoms) to the bond. When the exo-electron is transferred to the sigma bond, the bond is destabilized. If an electron donor (nucleophile) is near enough, it supplies one electron to the now vacant exo-sigma orbital, IF the redox potential is sufficient to allow such a transfer. When this occurs, the electron in the sigma bond can no longer return to the exo-sigma orbital. The destabilized sigma bond now dissociates with the leaving group taking the electron. The electronic structure of the nucleophilic center now reorders with Walden inversion of the attached atoms as the nucleophile continues forward to form the new bond. The SN2 reaction path is direction dependent and not microscopically reversible after electron transfer! Even if the atoms could take a microscopic step backwards, such a move would be insufficient for the electron to overcome the electrode potential required for its transfer back to the nucleophile. Thus, microscopic reversibility and path-independence as pertains to the Transition State is a highly improbable event is SN2 reactions.
New 2-D designs for representing the currently accepted and MCAS models are presented.