Miscellaneous calculations
In the absence of a good Monte Carlo, here are some back-of the-envelope calculations

I - Acceleration using a launch tube

Assume: The upward force at launch is equal to the pressure times the area of the nozzle.
The area is 3.46 cm^2
The pressure is 70 psi = 31.8 kgf/sq.in = 4.93kgf/cm^2 = 48 N/cm^2
Therefore the upward force on the bottle is 167 Newton. The mass of the bottle + water is 0.77 kg, so the acceleration is 217 m/s^2, which is 22 g. This acceleration is roughly constant until the bottle rises above the launch tube.

Assuming the launch tube is 20 cm long, the bottle will clear the top of the tube after 43 ms, at a velocity of 9.3 m/s, which is 21 mph.

II - Acceleration without a launch tube.

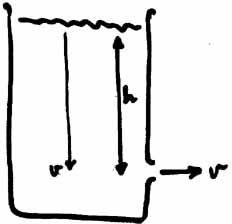In this case the water is forced out of the bottle opening immediately after launch. How fast would it be flowing? I use the following approximation: Suppose I have a vessel, filled with water, which has a hole in the side a distance h below the surface of the water. How fast does the water flow out of the hole? The answer is that the outflow velocity v is equal to the velocity of a freely falling object falling from the same height h.

So what is the height h such that the pressure at the hole is 70 psi or 48 N/m^2?

Last update 18 February 2004
HvH


back