Fun with small numbers
| I have noticed that students in every grade are not fluent with arithmetic facts and
operations. This
forms a barrier to developing current-level math skills. Kenken puzzles offer a fun way to
develop this fluency.
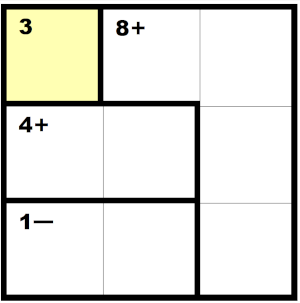
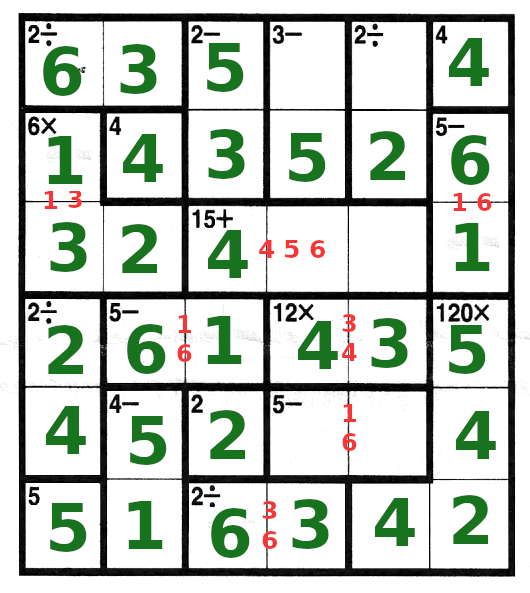
If you're not familiar withn Kenken puzzles, here is an example
| |
| First the freebies:
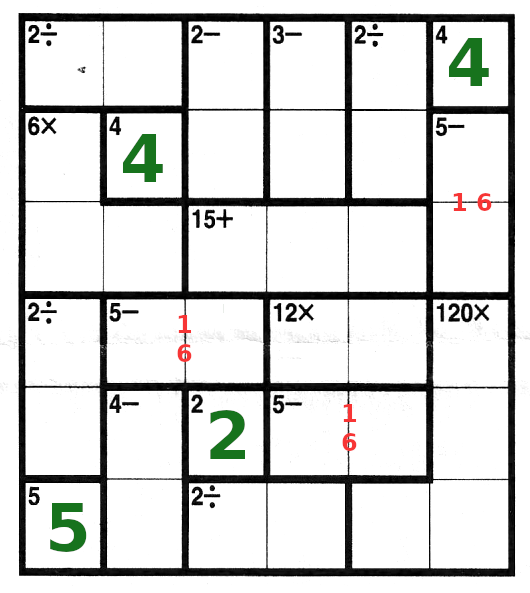
- 4 in the top row - 4 in row 2 - 2 in row 5 - 5 in row 6 Next, look at the box pairs with "5-". How can we make a five, by subtracting numbers 6 and under? Only one way, namely 5=6-1. Therefore we can pencil in 1 and 6 in between the 2 boxes | 
|
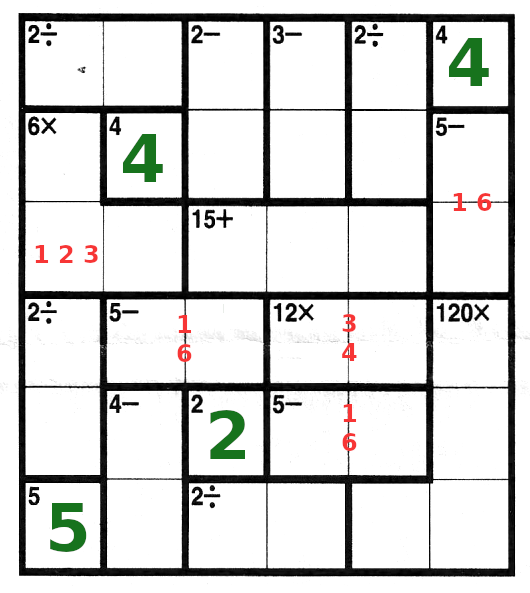
| Look at the L-shape, that makes 6 by multiplication. How can you make 6 by multiplying?
6 = 1x1x6 or 6=1x2x3. The first one cannot be right, because of the 1 and 6 in the last column. No matter how you place the 116, there will always be a conflict. So this 6 = 1x2x3. Next, see the box pair that makes 12 by multipication. 12=2x6 or 12=3x4. But 2x6 does not work, because there already is a 6 in that row, so it had to be 3x4. What is now left to go in row 4? 1,6,3,4 are already taken, so only 2 and 5. 5 cannot go on the left side, because of the 5 on the bottom left. So now we can fill in 2 and 5 in row 4: | 
|
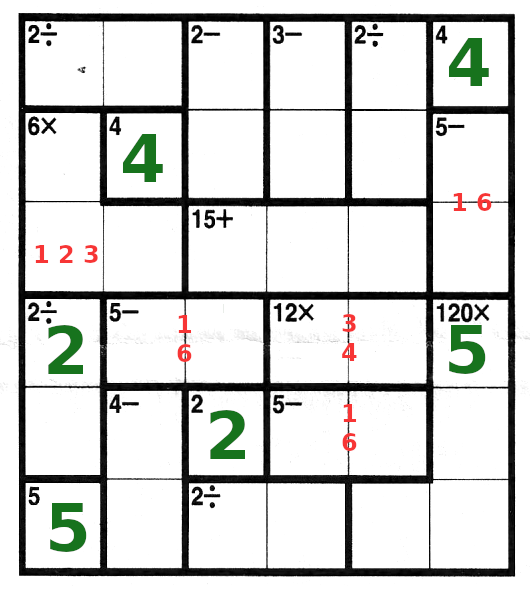
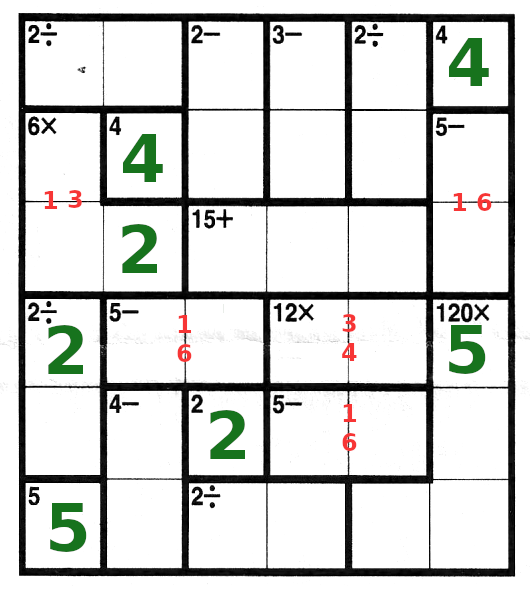
| Back to the 6=1x2x3. The 2 cannot go in column 1, so it goes in column 2 | 
|
| In column 1, 4 and 6 are not yet used. If 4 goes in the top left box, 6 goes in the 5th box down.
But 6/2 is not 2, so the six goes on top, and then 4/2=2.
On the top left we now have a 6, and 6/3 makes 2, so a 3 goes next to the 6 in the top row. | 
|
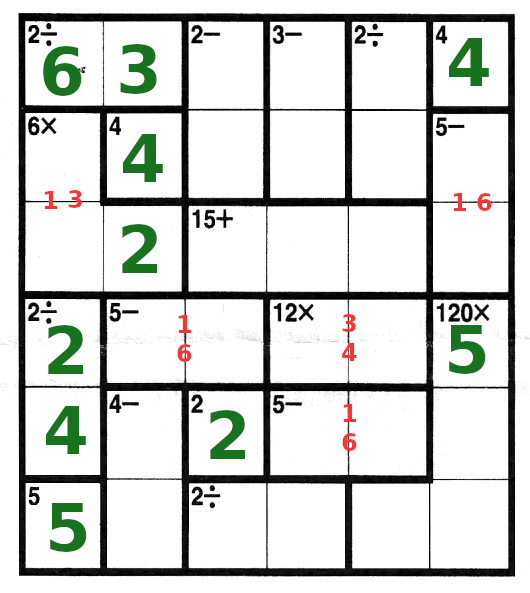
| In column 2, what is left is 1, 5 and 6. Can we make 4- from these? Yes, 4=5-1. So we can fill those in and also then the 6, and the 1 in column 3. | 
|
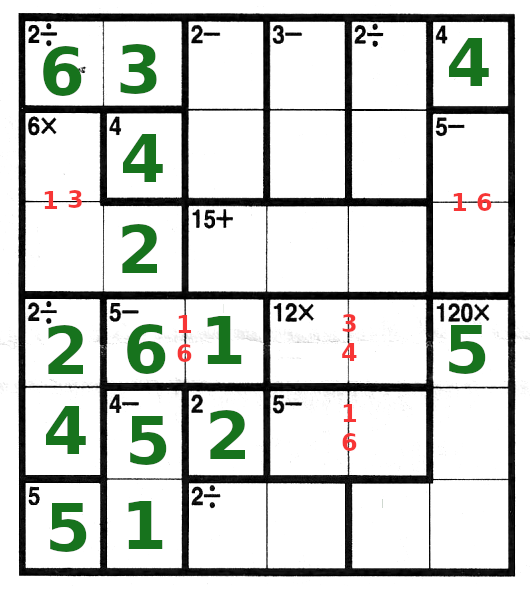
| what's left in the last column is a 2 and a 3. 2 has to go at the bottom right, 3 above it. 2x3x5 makes 30, and to get to 120, we have to have a 4 in the bottom row, column 5. | 
|
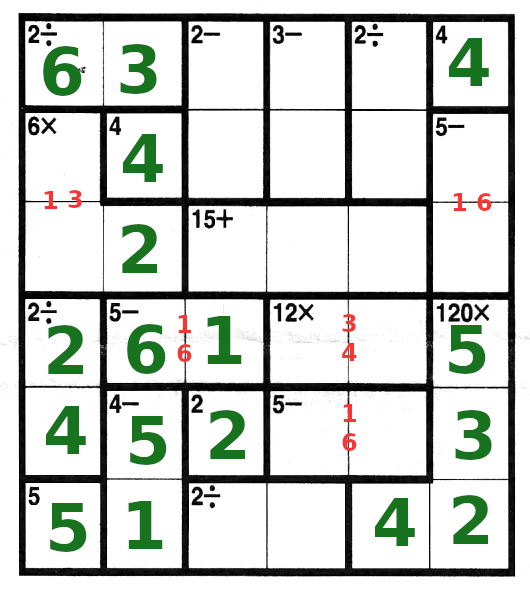
| Bottom row needs a 3 and a 6. | 
|
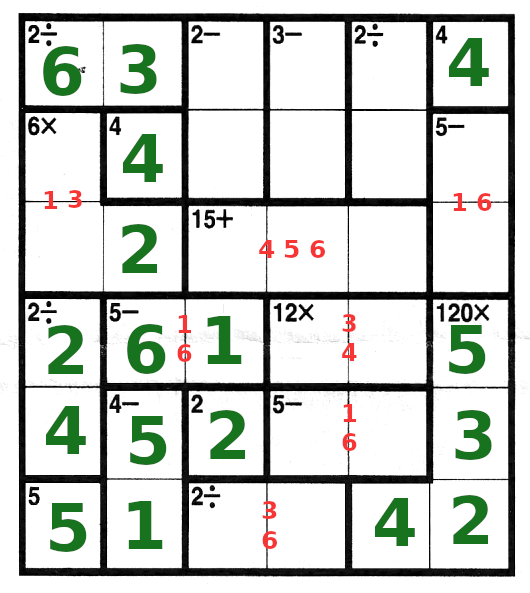
| Let's look at the 15+ box. First, there has to be a 4 in there somewhere. Notice that there already
are 4s in all rows except that third one.
Also, there has to be a 5 in there somewhere, since it cannot be elsewhere in row 3. Now 4+5=9, so we need a 6 to make 15. So the 15 box has 4,5,6 in it. Therefore we know how in the last column, 6 goes on top, and one below, and then in column 1, the 1 goes on top. | 
|
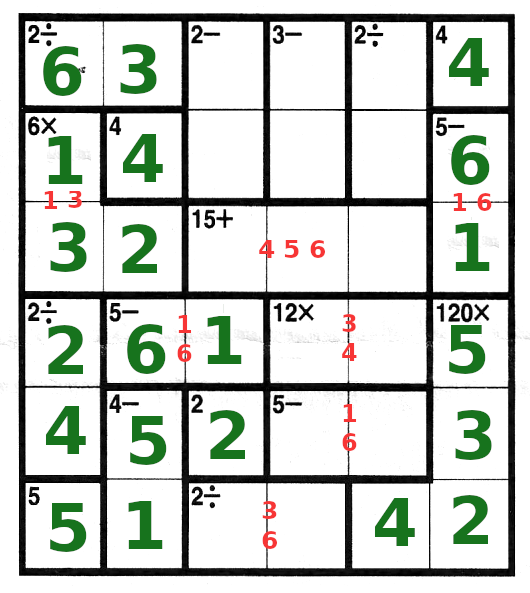
| In column 3, we have a "2-", and we have left the numbers 3,4,5,6. So we can make a 2- out of 5-3, or out of 6-4. But 6-4 is not possible because we already have 4s in rows 1 and 2. So is hass to be 5-3, with the 3 below the 5. | 
|
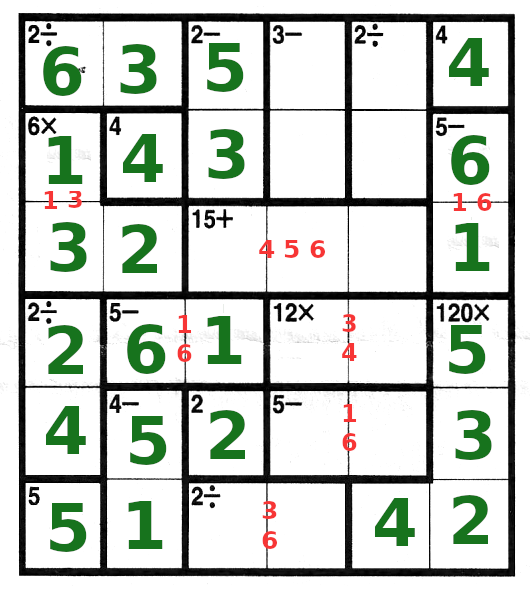
| What's left to do in the 3rd column is 4 and 6. But 4 cannot go in the bottom box, that one has to be 3 or 6, so we place the 4 and the 6. Because we placed the 6 in the bottom row, the 3 gets placed next to it, and because of that, we know how to place the 3 and 4 in row 4. | 
|
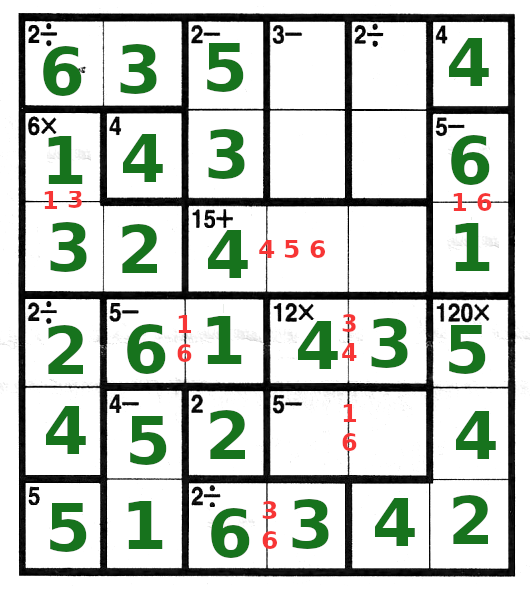
| We still need a 5 in row 2. But it cannot be in the "2/" box, because 5 is not divisible by 2, and 10 is too large. Therefore we can place 5 and 2 in row 2. | 
|
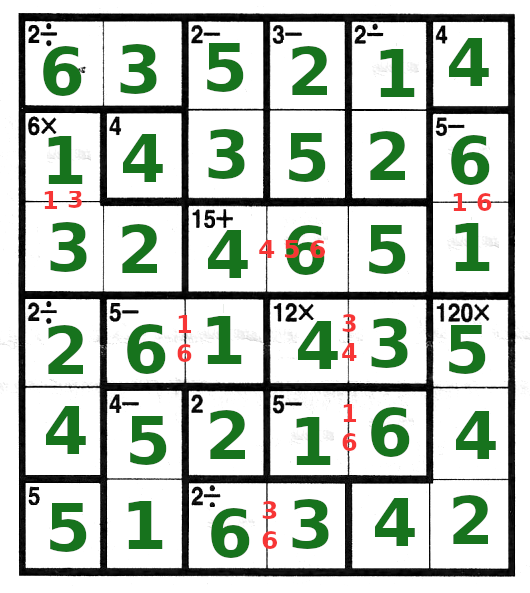
| With that, we can solve the rest: 5-2=3; 2/1=2; and everything alse falls into place. | 
|
| |
Here are some more 6×6:
| Here is a simpler one, 3×3: | 
|
| and some more: (2), (3), (4), (5), (6), (7), (8), (9), (10) | |
