Based on that, I built the contraption shown on the right. The grounded sphere is suspended from one arm of a sensitive balance, and a counterweight is suspended from the other end. The counterweight is a can filled with enough screws to balance the sphere, plus a few (Order 10g) grams more. The can rests on my electronic kitchen scale.
In the picture, I have highlighted the (thin, non-stretch) string that runs up from the sphere, over two small nails on the balance arm, and down to the can, where it is tied with a simple knot.
The measurement procedure is as follows:
- Untie the knot at the can, and re-tie it higher or lower. This raises or lowers the grounded sphere.
- Level the balance arm such that the horizontal part of the string is parallel to edge of the roof.
- Zero the scale
- Turn on the VDG, and see the scale readings change to a negative value
- When the reading stabalizes, record the value.
- Discharge the VDG, and measure the distance between the spheres.

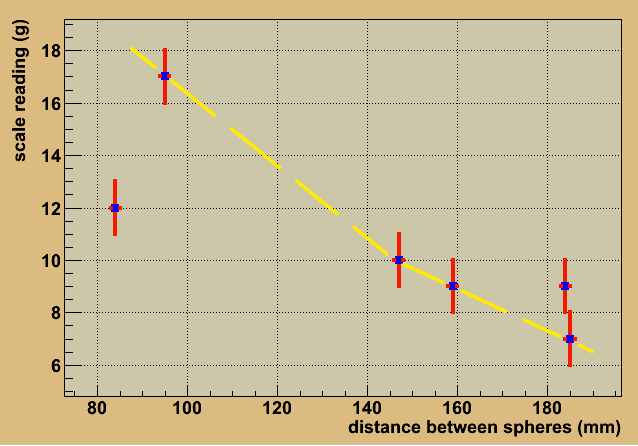
distance between scale
the spheres (mm) reading
-------------------------
77 spark at 20g
116 spark at 16g
84 12g
147 10g
184 9g
184 7g
159 9g
95 17g
62 spark -
85 spark -
119(?) 17g
-------------------------
Ambient conditions on 28 Dec 2014: 32°F, 33% relative humidity, sunny,
no wind.
Big sphere: 11" diameter → R1 = 14 cm.
Small sphere 38 cm circumference → R2 = 6.0 cm.
plot script
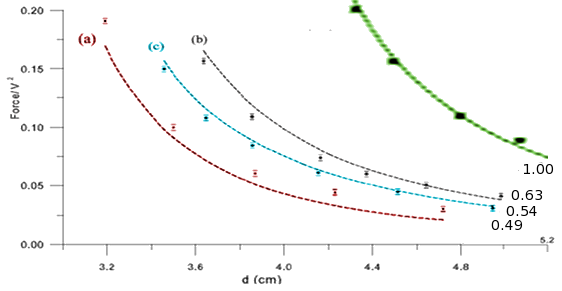
1) Cruz and Ley-Koo: Evaluation and measurement of forces between two conducting spheres
This paper had calculations as well as measurements. I overlayed plots for different ratios between sphere radii. Our spheres have a ratio of 0.43, which turns out to be a very large extrapolation from the published curves.
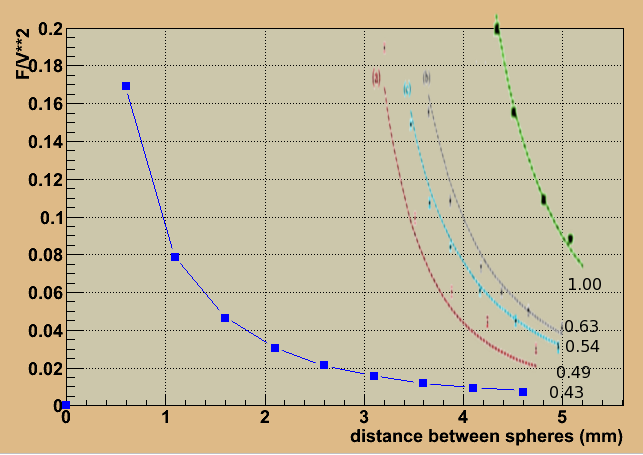
and
Lekner: Electrostatics of two charged conducting spheres
and
Electrosttic interaction between two conducting spheres
and
Lekner: Electrostatic calibration of sphere-sphere forces
and
Lekner: Electrostatics of two conducting spheres
and Electrostatic force between two conducting spheres at constant potential difference
