Click image for free 18Mb pdf of this "out-of-print" book

This article and others are included in the 18 chapters of "Rethinking the Atom" a 164 page paperback compilation of articles by JMW $19.95 US list at Amazon Click here  for Amazon.com

Click image for free 22Mb pdf of the book

If a ray of sunlight hits the retina of your eye, can the sun itself exist in your eye? In other words, what is the probability that the sun is actually in your eye? Is this probability really finite? In the vernacular of quantum probability, the answer would be yes! Where is the flaw in this logic?

Consider the same situation with an electron. If a tiny bit of negative field is detected, does it mean that an electron has a finite probability of being there or ever has been there in the context of the matter studied? If an electron were held in-place (physics thought experiment), it would have a surrounding field whose strength would be inversely related to the distance from the electron squared (r2); see the figure at the right. Would anyone deem that the electron is anywhere in these zones and even beyond as depicted in a dot representation like that just to the right? The sharpness and constancy of observed spectral lines when electrons move from one energy level to another would be most unlikely from such randomness to other such randomness. But, this is the reasoning of QM atomic probability modeling. Fortunately, experimental evidence[,1,2 ] is demonstrating that electrons are particulate at the nucleus level and have orderly behavior in orbitals. Consequently, random dot representations of electrons in atomic and molecular orbitals need to be put aside.[1,2 ]

Orbitals are deemed to contain the motion of electrons about a nucleus. In this way, they contain a collection of electron orbits. If electrons move around a nucleus, their motion is likely to be contiuous, closed-loop, and eliptical. The MCAS model possesses these characteristics. The MC mirrored orbital pair of this model is illustrated at the right. Electrons move from orbital to orbital within a tetrahedral set in the style of a hypotrochoid.[ 3] From this figure, the reader should get the impression that electron behavior around a nucleus is precise and not a nebulous cloud.

The reader can get a feel for the movement of an electron on a closed loop in the video on the right. The swf file is set for play and loop. Clicking on it you should be able to hit play and stop it. The electron with a diminishing field (3D actually, but shown in the video as a plane) is moving in a tear shaped path. The electron in the video is on a single lobe path. In the MC model, it will pass through each of the 3 other lobes of a tetrahedral unit before returning to this one to complete the circuit. An orbital should be about the expanse of negativity as well as actually containing an electron; i.e., it should contain most of the electrostatic field of an electron as it repeatedly moves in its appointed path around the nucleus. In some video players, the moving field begins to streak.

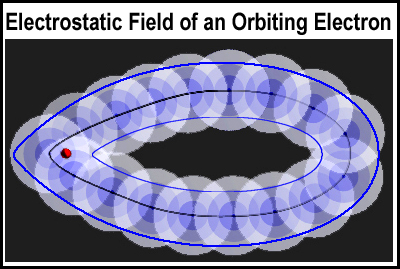Since electrons move at nearly the speed of light, the electron will create a nearly continuous presence of its electrostatic field. A feel for that continuum is presented in the figure at the right where 17 locations are shown. The electron is following the black middle path. Some posit that an orbital contains the electron 90-95% of the time. A counter position is that the orbital contains the electron all of the time and that it is only the lessened magnitude of the electrostatic field that is outside of the orbital and not the electron itself. The outer bound of the orbital would thus be the outer blue line. The presence of a small amount of negative charge is not the same as an electron possibly being at that point (vide supra).

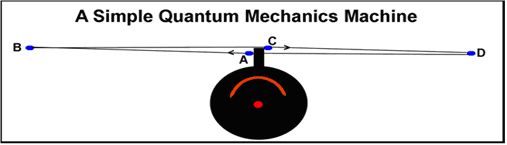The energy levels of the orbitals of a hydrogen atom are scale as the square of integers from 1 upwards. This is predictable from classical physics! A simple “quantum” machine (shown in the figure on the right) is sufficient to explain why this happens. The explanation has been presented elsewhere[ 4]; the article can be accesssed easily by clicking here. The relationship of this “quantum machine” to the orbital movement in the video should be obvious. For a tetrahedral MC unit, the four orbital extremes will be BDBD.

Have you ever considered that atomic orbitals could be hollow? That is how the experimental results could be interpreted.[1,2] In an analogy to the outer limit of the orbital, a thin blue inner line is drawn in the figure above. While the electrostatic field of a electron decreases “forever” (the connecting fabric of the universe?), its magnitude could be very small in the middle of the orbital. It seems quite reasonable to think of an electron orbital as a “fleshy, hollow pod”. Since an electron follows a precise path dictated by its electrostatic interactions with the nucleus and other electrons, the orbital path will be flattened and pad-like; similar to a spineless, prickly pear cactus stem shrunken in the middle. Another analogy would be a “pulled” torus. Without knowing where the path is, a cone with a single scoop of icecream provides the reasonably good orbital exterior that I used in the MC mirrored orbital pair figure.

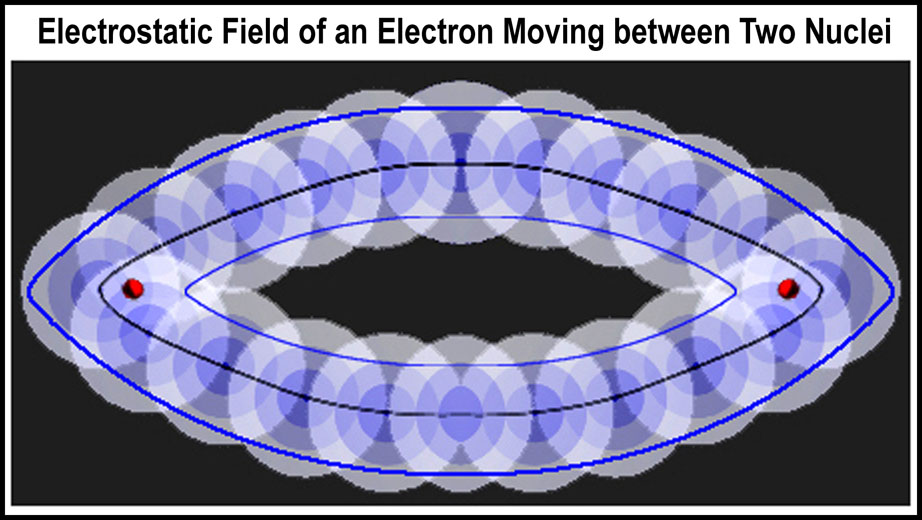The figure on the right is a combination of two atomic orbitals to create a molecular orbital. In the current spdf-QM hybrid approach, this would be a sigma orbital.  Two electrons would be in the same orbital; here paired by movement in opposite directions instead of the spin-reversal premise of the spdf-QM model. In the MCAS model, the electrons continue on to the connected orbitals of the quartet before returning to this molecular orbital. Again, electrons are paired by reciprocal motion relative to a molecular center and not by electron spin-reversal. Note that there is NO actual electron presence on the axis between the nuclei. Two electrons would not go directly AT a nucleus; to do so, they would collide! Coordinated movement of electrons is more “Virginia Reel” than Brownian.

G.N Lewis pointed out in the early 1900s that simple, real, molecules followed a “rule-of-eight” and that the orthogonal projections of the p-orbitals and the spherical s-orbital of the spdf-QM model did not yield the observed molecular structures. The octet rule imagery, however, did give good indications of molecular form. This is the concept that the MCAS model of the electron orbitals is based on. At the elementary level, “tinker toy” stick models still provide the best, simple, “hands-on”, understanding of atomic interactions, in my estimation, with a caveat about just what those stick single and spring “double and triple” bonds actually are. I would add that the balls need 8 holes instead of the current 4 (just drill the current four holes straight through the sphere) with the tetrahedral quartets ringed with two different colors... The equivalent 2-D paper representations of “single”, “double’ and “triple” bonds are also quite useful to the chemist who is interested, for example, in replacing “the multiple bond” (electron-deficiency) between two atoms with a bond to each of them from other atoms.

SUMMARY

It is one thing to draw lobes for electrons with the understanding that one does not know what is going on inside those lobes. It is something entirely different to indicate that these lobes are filled with clouds or dots of electron presence and that, incidentally, some electrons will even be randomly present outside these lobes! With electrons being detected as particles around nuclei, wave/particle duality and probability models that indicate electrons can be anywhere and everywhere become less believable. The wave approach as an indication of an electron’s path is quite appropriate, however. The mathematical probability approach steers the scientific mind away from how electrons move and reside. An electron’s movement is well defined per the precise spectral data it generates. Movement to and fro between atoms will be on well-defined pathways with an electron’s electrostatic field moving with it.

We live in a society exquisitely dependent on science and technology, in which hardly anyone knows anything about science and technology. -- Carl Sagan

REFERENCES

1 A. S. Stodolna1, A. Rouzée, F. Lépine, S. Cohen, F. Robicheaux, A. Gijsbertsen, J. H. Jungmann, C. Bordas, and M. J. J. Vrakking, Hydrogen Atoms under Magnification: Direct Observation of the Nodal Structure of Stark States, Phys. Rev. Lett. 110, 213001 (2013)

2 Joel M Williams, Nixing the ‘Balloons-of-Electron-Dots’ Atomic Orbital Models, http://pages.swcp.com/~jmw-mcw/Nixing%20the%20'Balloons-of-Electron-Dots'%20Atomic%20Orbital%20Models.htm

3 Joel M Williams, Modeling the MCAS WAY, http://pages.swcp.com/~jmw-mcw/science; original at http://arxiv.org/html/physics/9902046v2

4 Joel M Williams, The Bohr Model, Electron Transfer and Newtonian-derived Quantum Numbers, http://pages.swcp.com/~jmw-mcw/MCAS/MCAS_Jai-Alai_and_the_Ballmer_Series.pdf