Abstract
Helium provides the simplest multi-electron atomic situation. Quantum
mechanics addressed the different magnetic property of ortho and para helium
with “mirrored twins”. This paper addresses that difference with
“mirrored rooms” – a different implementation of parity. Models
are provided to illustrate why each can not be converted to the other in a
single photon-induced step. These models also illustrate the vastly greater
orbital sizes of the excited states over the ground state. Included is a
reference to a paper demonstrating that classical physics provides the
physical mechanism by which an electron’s energy levels scale with n2.
The mirror-room orbitals would also be appropriate for non-classical
approaches without requiring spin-reverse pairing of electrons in the same
orbital.
INTRODUCTION
Back a century ago, scientists
worked diligently to explain the spectral data of excited atoms. These spectra
included S(harp), P(rincipal), D(iffuse), and F(undamental) lines that were to
be addressed. The main thrust of the physical model that continues to this day
got its start with Bohr’s orb. From this, “electron house” plans were
drawn: a “1-room bungalow” up gradable to a “4-room split level”.
Additional stories with 5 or 7-rooms were added to make “electron condos”.
The room plans got labeled: s (1), s+p (4), d (5), and f (7) or spdf for short.
Pauli mused that there was a problem of which occupant was which when the rooms
were double occupied and everybody needed an SS#. Heisenberg, who made
significant contributions to what became “quantum mechanics”,
came to his rescue when he wrote to Pauli in 1926 that e-spin might be the
solution to the ortho/para helium phenomenon
and thus to Pauli’s exclusion problem. So, “parity electron twins” that
occupied the same room (cell, orbital) were created. Some would say that ortho/para
helium proved the correctness of the quantum mechanics approach. QM certainly
stifled alternative views.
The “quantum mechanical –
spin-paired” model still is the accepted convention: n (floor level), ℓ
(room shape), m (wing), and s (left or right-handed twin in the double bed) are
the notations that define an electrons place in the double-occupancy spdf rooms.
While the mirroring of electrons (“mirrored twins”) can be handled by
mathematics, it is still not clear just how it happens in our physical world
where electrons repel one another. It would have made more sense to have
mirrored the rooms that were singularly occupied, but that option was eliminated
when the lowest room in any condo had to be a centered sphere.
Scientists are now developing
techniques to investigate electrons at the nanometer level.
Helium will likely be the next atom studied. To provide an alternate
particle approach to the current QM electron orbital model, a “mirrored
room” model is applied to para and ortho helium.
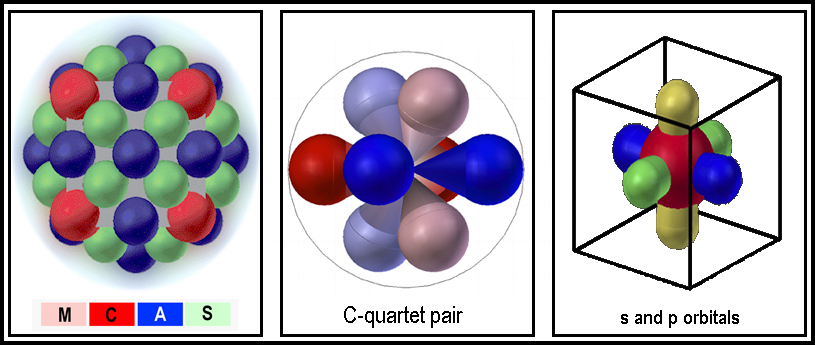
A “MIRRORED ROOM” ELECTRON ORBITAL
MODEL
A “mirrored-room” equivalent of a sphere is easily envisioned. It is
simply two, diametrically opposed tetrahedral-lobed spaces with a common center.
Each orbital lobe can contain a single electron. When the orbitals are so small
that e-repulsions between electrons would make filling all of them prohibitive,
only one electron occupies each quartet; this is the case for hydrogen and
helium. As the orbital sizes increase (increased energy), all of the orbitals
can contain an electron; e.g., neon. Not only does this “mirrored- room”
equivalent replace a sphere, it is also equivalent to the s+p, split-level
group. This is the MCAS model.
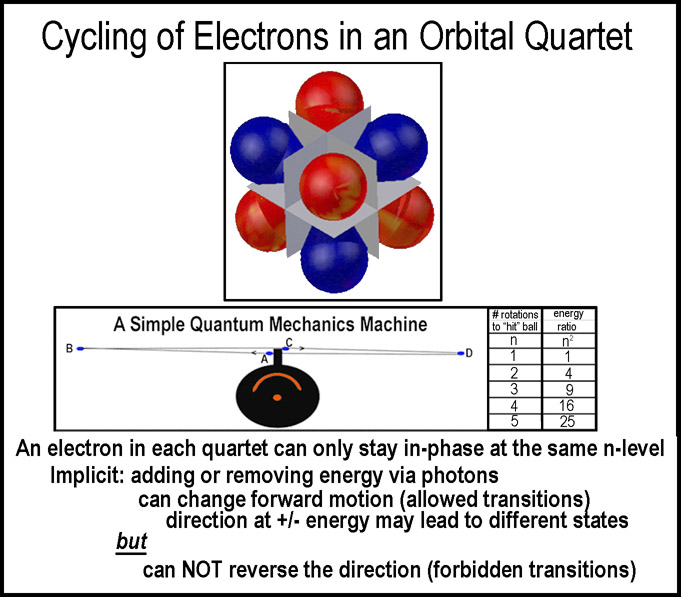 A
simple quantum mechanics machine (shown at the right and discussed elsewhere)
indicates, a priori, why the excitation levels scale by n2. Implicit
in the model is movement and coordination with the nucleus. The
"mirrored-room" orbitals are simply that: orbitals; a different, but simpler
set that explains the physical data and the periodic table. They would also be
appropriate for non-classical approaches without electron-pairing should stanch
adherents to the non-classical get past their objection to the fact that these
orbitals can satisfy classical physics as well!
A
simple quantum mechanics machine (shown at the right and discussed elsewhere)
indicates, a priori, why the excitation levels scale by n2. Implicit
in the model is movement and coordination with the nucleus. The
"mirrored-room" orbitals are simply that: orbitals; a different, but simpler
set that explains the physical data and the periodic table. They would also be
appropriate for non-classical approaches without electron-pairing should stanch
adherents to the non-classical get past their objection to the fact that these
orbitals can satisfy classical physics as well!
At this point it is important to note the effect of adding and removing energy.
Adding energy to or removing it from an electron via photon addition or release
is like accelerating and decelerating a car with the gas pedal – there is no
effect on direction, per se. A reversal of direction by this action will not
happen. Moving to a higher or lower lobe of similar shape is the norm. Moving to
another orbital that has another shape is possible, if the direction of the
electron at the moment of energy change would send it there. Thus, an electron
can NOT move from a RED
M-orbital system to a BLUE
one or vice versa. This is a “forbidden” transition by a photon change. 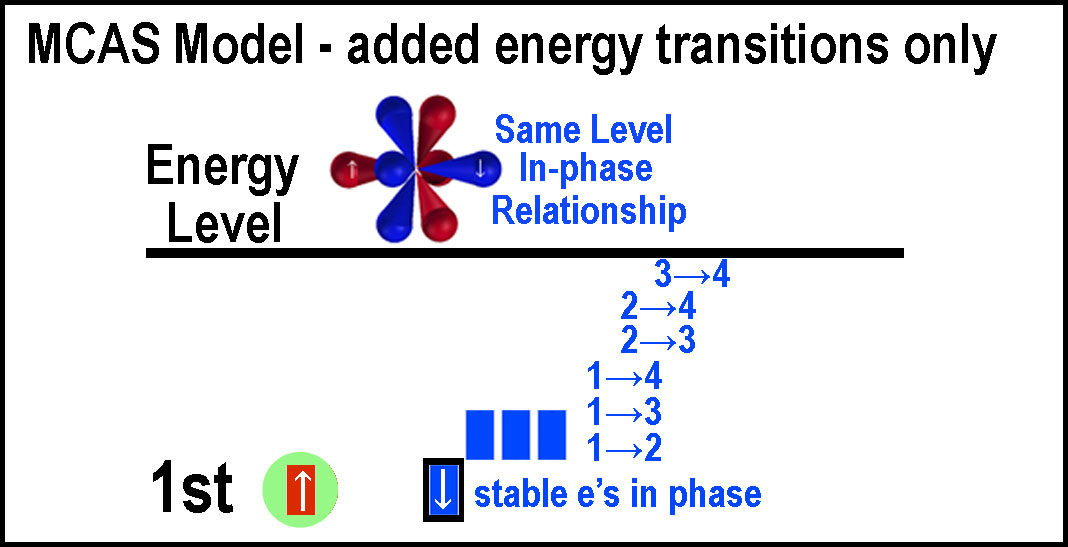 To
be “in-phase”, two electrons must remain diametrically opposite one another
or flowing in the same orbital group. To do this they need to be at the same
energy level (n). Otherwise the time to transverse orbital lobes will be
different. The “in-phase” state is the lowest for every energy level. Note
that there are 3 non-diametric options even at the “same” energy level for
the simple opposed quartets – these provide some fine structure before the
unstable system moves to the more stable diametrically opposed position through
energy loss. They provide a staging point for transitions and may even make one
electron appear more energetic than the other.
To
be “in-phase”, two electrons must remain diametrically opposite one another
or flowing in the same orbital group. To do this they need to be at the same
energy level (n). Otherwise the time to transverse orbital lobes will be
different. The “in-phase” state is the lowest for every energy level. Note
that there are 3 non-diametric options even at the “same” energy level for
the simple opposed quartets – these provide some fine structure before the
unstable system moves to the more stable diametrically opposed position through
energy loss. They provide a staging point for transitions and may even make one
electron appear more energetic than the other.
THE PHYSICAL SPACES OF ELECTRON
TRANSITIONS
 The
Bohr circles that indicate simple one-electron n-state transitions do not
indicate the magnitude of the energy involved in those transitions very well to
students by my reckoning. The figure at the right is intended to provide a
better feel. Note the tiny little first level circle.
The
Bohr circles that indicate simple one-electron n-state transitions do not
indicate the magnitude of the energy involved in those transitions very well to
students by my reckoning. The figure at the right is intended to provide a
better feel. Note the tiny little first level circle.
It is all a matter of the
transversing time needed to arrive back at the required appointment moment with
the nuclear regulatory checkpoint and pass on to the next lobe. The nucleus
keeps its roadies in line with firm discipline based on the constancy of the
spectral data. This raises the question as to when an electron can add or dump
energy: can it occur only when it passes the nucleus, at some other place, at
many places, everywhere? Do atoms have drive-through pump and dump stations? Is
there “in-the-air” service like the military does for non-landing planes?
Knowing how electrons and nuclei interact would be quite valuable information
for a more complete understanding.
THE ENERGY STATES OF
PARA
AND ORTHO HELIUM
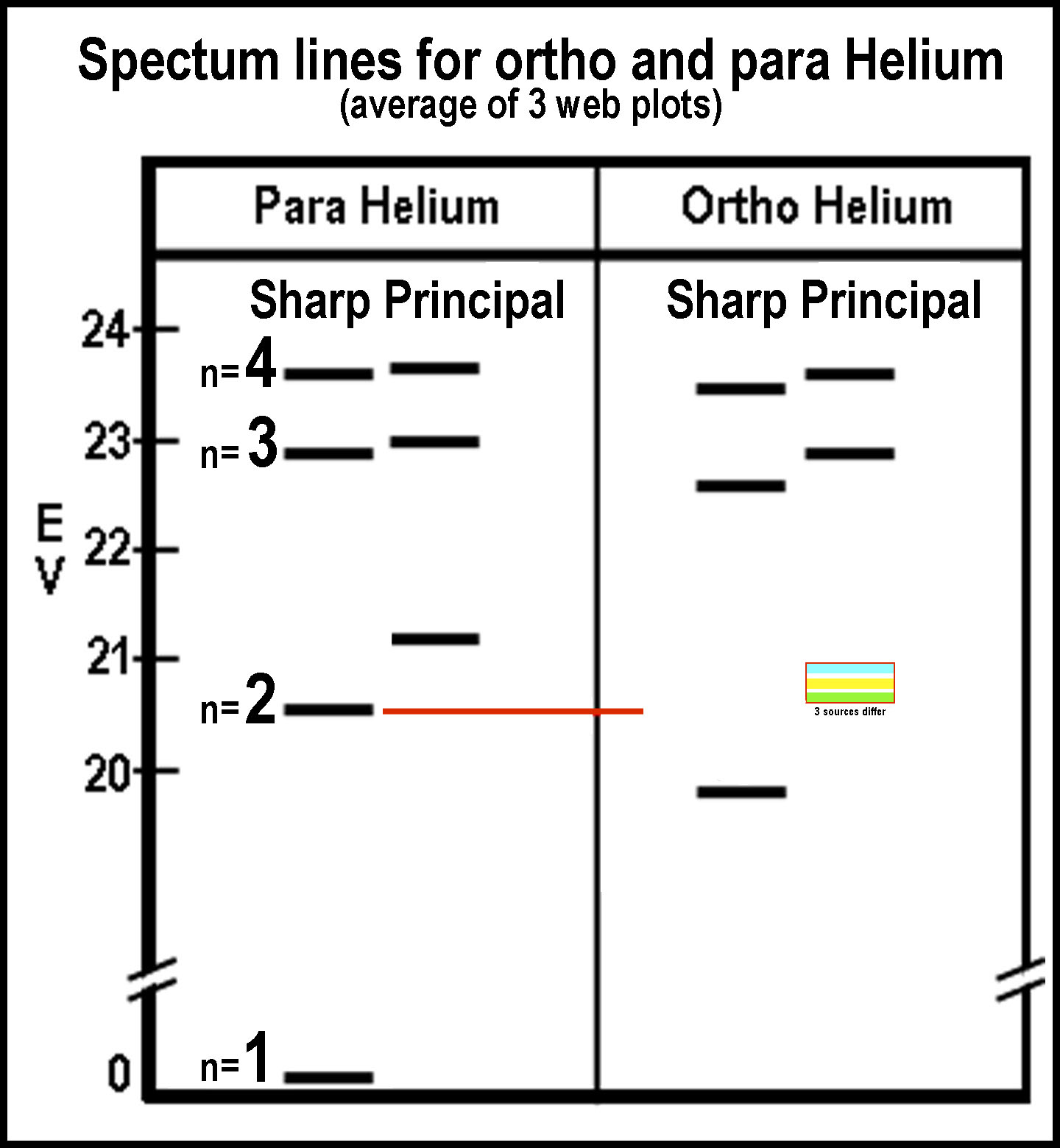 The
figure at the right is a composite of energy levels from 3 web sources.
The data was consistent up to the 4th n-level, except for the 2nd
level ortho “P”, where none agreed, but differed not greatly. S and P are
spectral assignments and, of course, in the quantum mechanical model, they also
represent that model’s orbital descriptions. Other energy levels and orbitals
are omitted here in order to focus attention on the first levels of energy
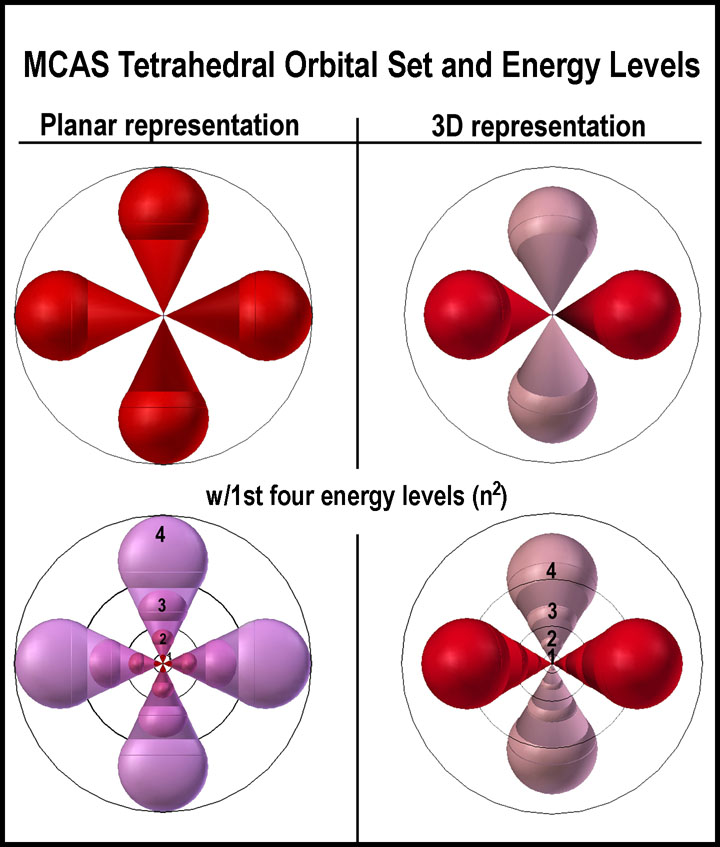
changes. S and P are handled by the C-orbitals of the MCAS model. The full MCAS
model of orbitals is given below: an M-orbital is a mono-occupied C-orbital
quartet. The sp orbitals of the spdf model are given for comparison.
The
figure at the right is a composite of energy levels from 3 web sources.
The data was consistent up to the 4th n-level, except for the 2nd
level ortho “P”, where none agreed, but differed not greatly. S and P are
spectral assignments and, of course, in the quantum mechanical model, they also
represent that model’s orbital descriptions. Other energy levels and orbitals
are omitted here in order to focus attention on the first levels of energy
changes. S and P are handled by the C-orbitals of the MCAS model. The full MCAS
model of orbitals is given below: an M-orbital is a mono-occupied C-orbital
quartet. The sp orbitals of the spdf model are given for comparison.
.jpg) Elevation
of the ground-state of para-helium to the next lowest energy level occurs in two
steps without changes in electron spin. In the first step, one electron is
elevated. This leads to a high energy, unbalanced, out-of-phase state. Part of
the energy in this state is utilized in the elevation of the second electron.
This gives rise to a balanced, in-phase state that has a lower total energy. In
the vernacular of chemical reaction mechanisms, the out-of-phase state is a
high-energy transition state, or an approximately equivalent meta-stable state.
In essence, the energy to promote the two electrons in the n=1 in-phase state to
the n=2 in-phase state is less than that required to promote one electron from
the n=1 state to the n=2 state. To return to the ground state, the process is
reversed.
Elevation
of the ground-state of para-helium to the next lowest energy level occurs in two
steps without changes in electron spin. In the first step, one electron is
elevated. This leads to a high energy, unbalanced, out-of-phase state. Part of
the energy in this state is utilized in the elevation of the second electron.
This gives rise to a balanced, in-phase state that has a lower total energy. In
the vernacular of chemical reaction mechanisms, the out-of-phase state is a
high-energy transition state, or an approximately equivalent meta-stable state.
In essence, the energy to promote the two electrons in the n=1 in-phase state to
the n=2 in-phase state is less than that required to promote one electron from
the n=1 state to the n=2 state. To return to the ground state, the process is
reversed.
With ortho-helium, the two
electrons are in the same orbital quartet. Readers who are familiar with
chemistry will recognize the ortho (adjacent) and para (opposite) placement of
the arrows in the two “n=2 in-phase” images in the figure. Having two
electrons in the same orbital quartet at the n=1 level is energetically
prohibitive. Thus, the lowest state for two electrons in the same orbital
quartet is at the n=2 level. This is the reason that lithium starts the second
row of the periodic table.
As in the case with para-helium, a higher energy state can occur with one of the
electrons dropping down to the n=1 level. Unlike in the para case, however, the
second electron can not drop down.
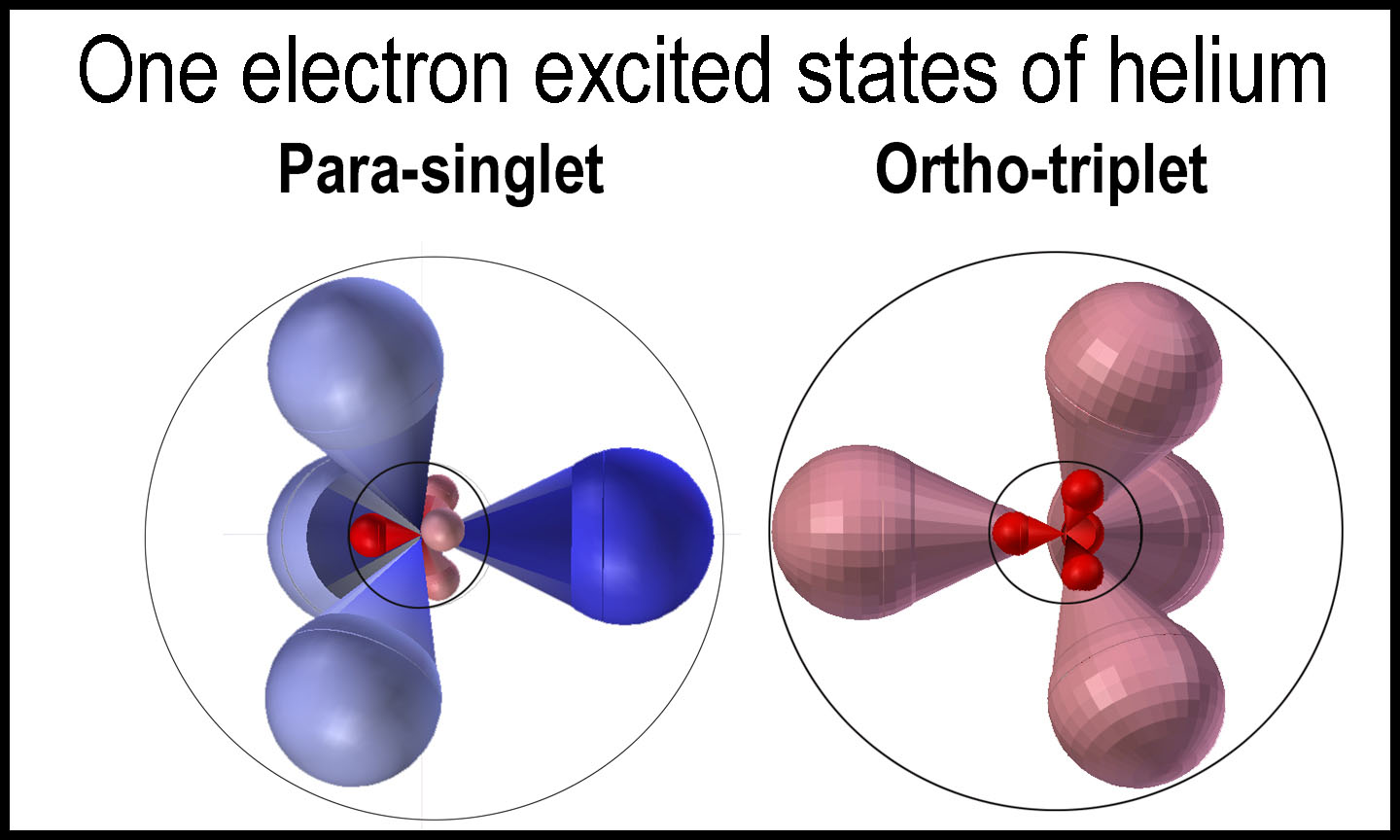 At
first glance, it would seem strange that the ortho-state is lower in energy than
the comparable para-state. Consider the figure on the right. The overall
electron interactions are just greater in the para-state than in the ortho state
as they move through the orbitals and go through nuclear “supervision”.
At
first glance, it would seem strange that the ortho-state is lower in energy than
the comparable para-state. Consider the figure on the right. The overall
electron interactions are just greater in the para-state than in the ortho state
as they move through the orbitals and go through nuclear “supervision”.
The second electron in ortho-helium
can not reverse direction under photon action and, thus, allow it to convert to
the para arrangement. The conversion of one state to the other will not occur
with the simple addition or removal of photon energy as a reversal of direction
is needed. Strong magnetic fields are needed to align the electron orbitals
(electron flow) to pair them and collision impacts are needed to reverse them.
SUMMARY
The "mirrored-room",
MCAS, orbital model provides an excellent explanation for the difference between
ortho and para helium. Spin-pairing is accomplished through movement through
opposing orbital units rather than through the "mirroring of
electrons" in the same orbital space as is done in the spdf model. The MCAS
model clearly demonstrates why ortho and para helium are not converted from one
to another with photon energy. The model also demonstrates that electrons are
operationally connected to one another as they pass by and coordinate with the
nucleus. They do not exist as clouds of negativity, although they emit negative
fields. Energy levels are related to "coordinated junctions" near the
nucleus and scale according to classical acceleration and deceleration laws of
electron velocity and their related electrostatic attractions (and repulsions?)
with the nucleus and repulsions with other electrons.
The MCAS model demonstrates that the lowest (n=1) energy level of atoms can only
have two electrons moving in opposite directions (paired) and can not have
electrons flowing in the same orbital quartet. This explains why the periodic
table begins a new period after helium with a higher energy, more spatially
expanded, set of orbitals which does allow additional electrons to occupy the
same quartet. The rationale for G.N. Lewis’ "rule of eight" is quite
clear with the eight-equivalent lobes of the "mirrored-room" model.
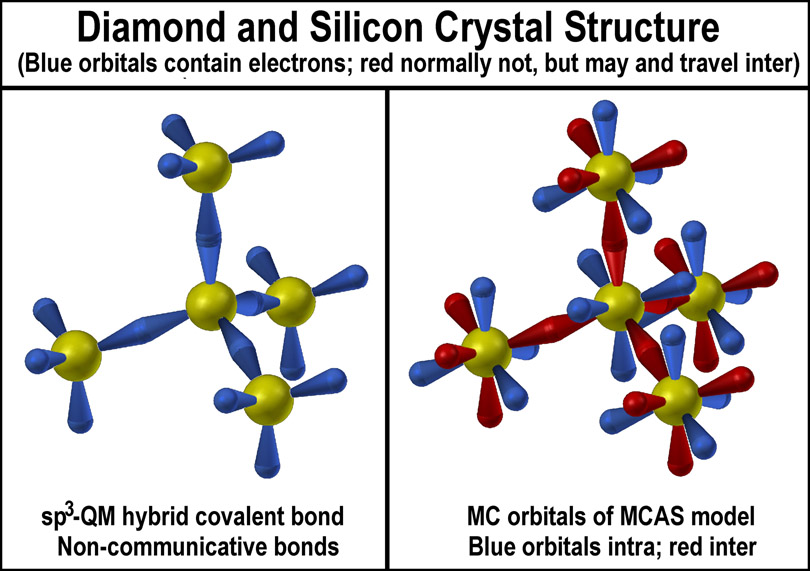
The MCAS "mirrored-room" electron orbital model offers the simplest
explanation for this and many other atom-atom interactions and does so without
having to "hybridize" orbitals to make compounds and
"reverse" the actual spin of electrons to effect pairing.
![]()
![]()



 A
simple quantum mechanics machine (shown at the right and discussed elsewhere
A
simple quantum mechanics machine (shown at the right and discussed elsewhere To
be “in-phase”, two electrons must remain diametrically opposite one another
or flowing in the same orbital group. To do this they need to be at the same
energy level (n). Otherwise the time to transverse orbital lobes will be
different. The “in-phase” state is the lowest for every energy level. Note
that there are 3 non-diametric options even at the “same” energy level for
the simple opposed quartets – these provide some fine structure before the
unstable system moves to the more stable diametrically opposed position through
energy loss. They provide a staging point for transitions and may even make one
electron appear more energetic than the other.
To
be “in-phase”, two electrons must remain diametrically opposite one another
or flowing in the same orbital group. To do this they need to be at the same
energy level (n). Otherwise the time to transverse orbital lobes will be
different. The “in-phase” state is the lowest for every energy level. Note
that there are 3 non-diametric options even at the “same” energy level for
the simple opposed quartets – these provide some fine structure before the
unstable system moves to the more stable diametrically opposed position through
energy loss. They provide a staging point for transitions and may even make one
electron appear more energetic than the other. The
Bohr circles that indicate simple one-electron n-state transitions do not
indicate the magnitude of the energy involved in those transitions very well to
students by my reckoning. The figure at the right is intended to provide a
better feel. Note the tiny little first level circle.
The
Bohr circles that indicate simple one-electron n-state transitions do not
indicate the magnitude of the energy involved in those transitions very well to
students by my reckoning. The figure at the right is intended to provide a
better feel. Note the tiny little first level circle. The
figure at the right is a composite of energy levels from 3 web sources
The
figure at the right is a composite of energy levels from 3 web sources
.jpg) Elevation
of the ground-state of para-helium to the next lowest energy level occurs in two
steps without changes in electron spin. In the first step, one electron is
elevated. This leads to a high energy, unbalanced, out-of-phase state. Part of
the energy in this state is utilized in the elevation of the second electron.
This gives rise to a balanced, in-phase state that has a lower total energy. In
the vernacular of chemical reaction mechanisms, the out-of-phase state is a
high-energy transition state, or an approximately equivalent meta-stable state.
In essence, the energy to promote the two electrons in the n=1 in-phase state to
the n=2 in-phase state is less than that required to promote one electron from
the n=1 state to the n=2 state. To return to the ground state, the process is
reversed.
Elevation
of the ground-state of para-helium to the next lowest energy level occurs in two
steps without changes in electron spin. In the first step, one electron is
elevated. This leads to a high energy, unbalanced, out-of-phase state. Part of
the energy in this state is utilized in the elevation of the second electron.
This gives rise to a balanced, in-phase state that has a lower total energy. In
the vernacular of chemical reaction mechanisms, the out-of-phase state is a
high-energy transition state, or an approximately equivalent meta-stable state.
In essence, the energy to promote the two electrons in the n=1 in-phase state to
the n=2 in-phase state is less than that required to promote one electron from
the n=1 state to the n=2 state. To return to the ground state, the process is
reversed.
 At
first glance, it would seem strange that the ortho-state is lower in energy than
the comparable para-state. Consider the figure on the right. The overall
electron interactions are just greater in the para-state than in the ortho state
as they move through the orbitals and go through nuclear “supervision”.
At
first glance, it would seem strange that the ortho-state is lower in energy than
the comparable para-state. Consider the figure on the right. The overall
electron interactions are just greater in the para-state than in the ortho state
as they move through the orbitals and go through nuclear “supervision”.