ABSTRACT
The
currently accepted, QM, spdf electron model is a collection of individual
orbital sets designed to handle 1, 3, 5 and 7 groupings. For anyone who takes
enough chemistry, these mathematically generated images are some of the most
memorable – as separate presentations, that is. When
combined in 3D space to contain 32 electrons, they are a mess as the sets are
not orthogonal to one another; nor are they dynamic. The spdf orbital sets,
their shapes, orientations, and spatial overlapping are addressed.
INTRODUCTION
The spdf orbital model of the
electrons of the elements of the periodic table is now over a century old. As
such, it is deeply entrenched in scientific studies. The individual components
(s, p, d and f) are presented in graphic form for all to grasp. They form some
of the most recognizable images of the scientific arena. Individually, that is.
Images of them combined in 3D beyond the s+p level are seldom the case. This
paper has been prepared to address that issue and to illustrate how these individual
components collectively handle 32 electrons.
THE spdf MODEL
The s, p, and d orbitals are
quite familiar to anyone who has studied the electronic structure of atoms. The f-orbitals, on the
other hand, are not so familiar. Interestingly, while the s, p, and d orbitals
are presented as singular sets, there are two (2) sets in common usage for the
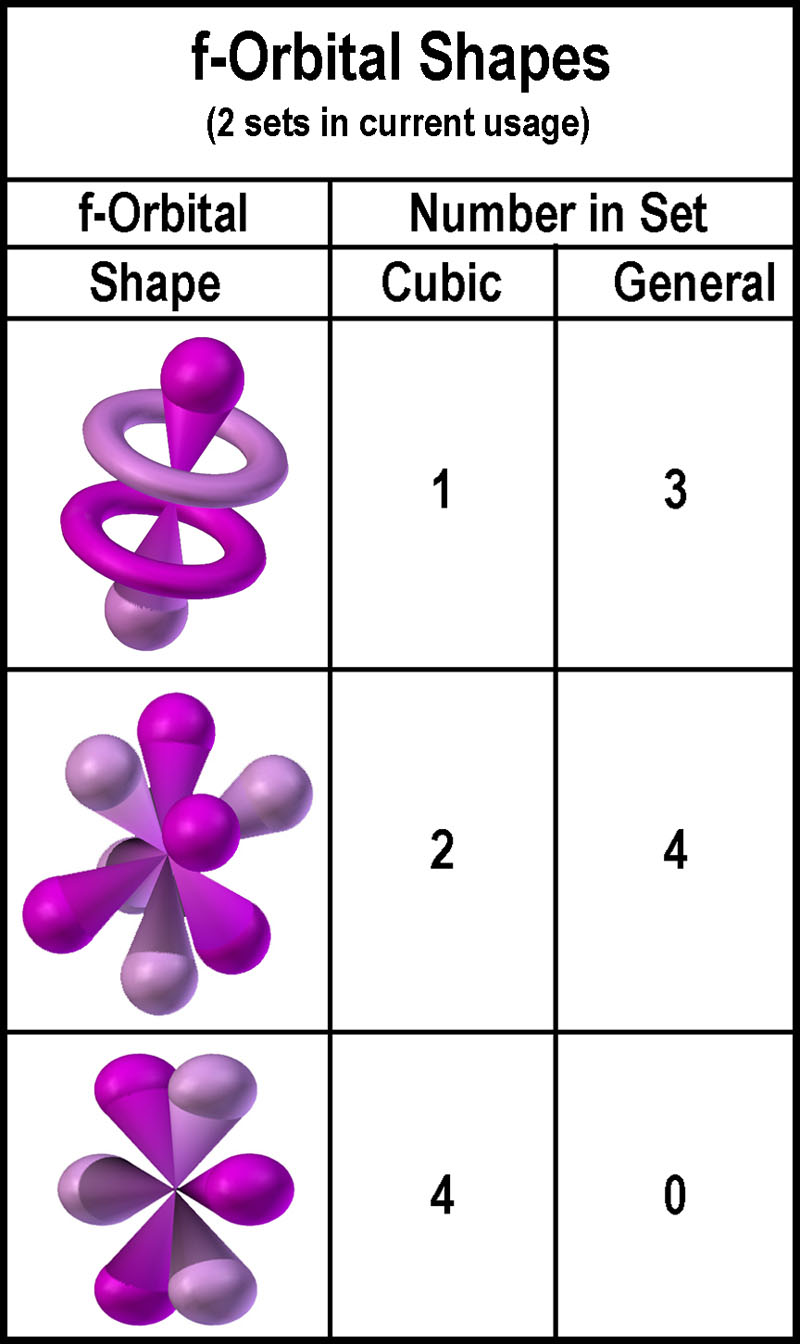
f-orbitals: cubic and general[1].
Images of both sets are found on the web with the cubic[2]
showing up more often than the general[3].
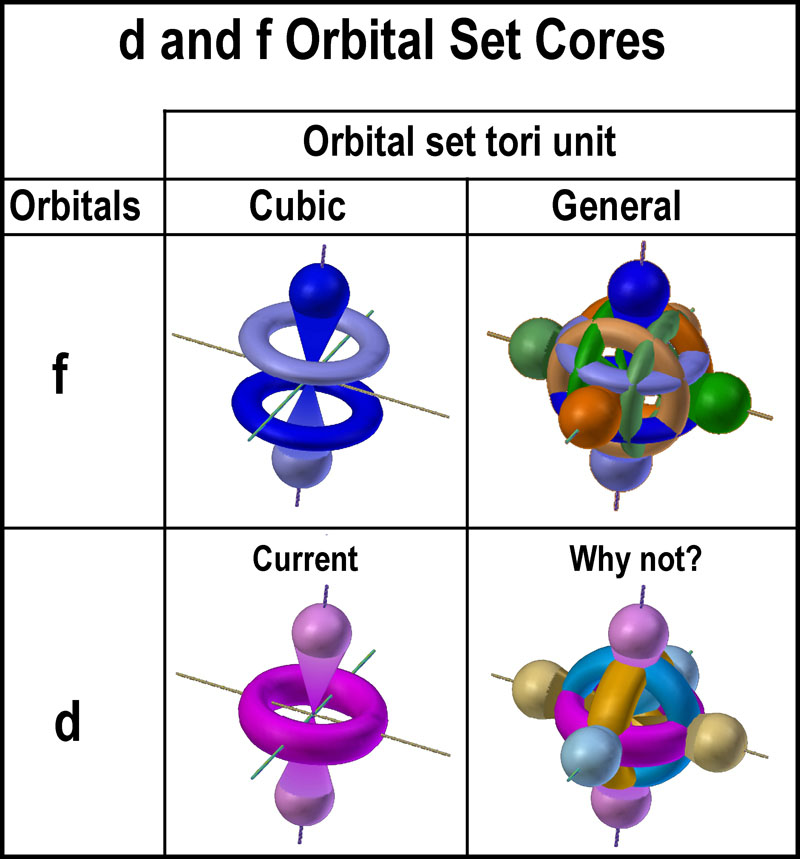
| The two f-orbital sets use the three (3) orbital shapes
shown in the figure at the right. Three are common to both sets[4].
The “cores” differ primarily in the number of “tori-orbitals” as
shown in the figure further right. The core of the general set gives the
illusion of a “gyroscope”[5].
Why isn’t a similar set presented for the d-orbitals? In other
words, why was one d-orbital set chosen over the other? |
|
|
The four common spdf orbital
sets are presented as artistic representations in the following chart in
typical, but inverted, “pyramidal” fashion along with d and f tri-torus
sets. The d-"Tri-torus" unit has 8 openings in the crossed tori. Only
2 "Planar, 4-lobed orbitals" can be accommodated. Thus, there are only
5 orbitals with a total of 14-lobes.
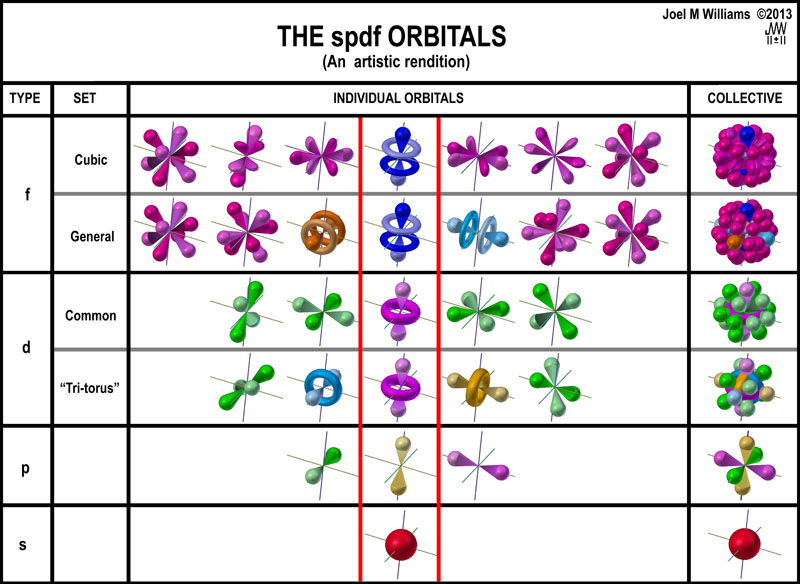
This layout of the spdf orbitals emphasizes
what the orbitals are intended to
do: model space for 1, 3, 5, and 7 pairs of electrons. What should be clear is
that each set ignores the fact that it starts
by occupying the space dedicated
to the
preceding one. This is seen in the center column of the above figure and
emphasized in the figure at the right. Roughly, the electron density of ~6
electrons, out of 32, is concentrated along this axis. With similar overlaps
along the x and y axes, ~60% of the total electron density of a period is
concentrated in ~20% of the spherical volume! This may be nice for mathematics,
but it is unlikely to occur in a real world situation.
dedicated
to the
preceding one. This is seen in the center column of the above figure and
emphasized in the figure at the right. Roughly, the electron density of ~6
electrons, out of 32, is concentrated along this axis. With similar overlaps
along the x and y axes, ~60% of the total electron density of a period is
concentrated in ~20% of the spherical volume! This may be nice for mathematics,
but it is unlikely to occur in a real world situation.
While they can handle the 1,
3, 5, and 7 pairs separately, they do not present proper orbitals when the sums
of the electrons are 2, 8, 18, and 32 as needed to address the periods of the
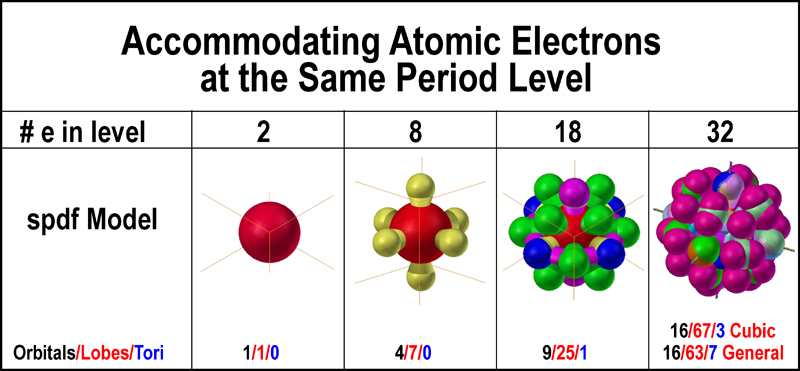
periodic table of elements. The following figure illustrates how the spdf
electron orbitals mesh to provide the number of electrons for a period in the
periodic table. The spdf orbital model starts with a “mild” overlap as the s
and p-orbitals combine to accommodate 8 electrons. The overlap is not so mild
when the d-orbitals are added to the s/p group to handle 18 electrons. [The
portions where the d-orbitals coexist with the px and py
orbitals are tipped with blue; a bit of yellow can be seen where the p-orbitals
are present. The pz orbital coexists with the purple dx2
orbital.] The overlap situation becomes extreme when the f-orbitals are added to
the s/p/d sum. [The general f-orbital set is used in the figure.] Of note is the
change in the number of lobes required to accommodate a pair of electrons: 1 for
2, 7 for 8, 25 for 18, and ~64 for 32 along with a few tori. Strange! Of course,
it is, but they have been mathematically generated according to the precepts of
the QM nlms numbers and fitting 5 or 7-component sets into 3D space using a
common origin.
The spdf model accommodates
additional electrons of the same period by having them occupy some of the space
already occupied by other electrons. Electrons are said to be able to coexist in
an orbital of a set (s, p, d, or f) through "spin-reversed pairing" -
one of the hallmark assumptions of quantum mechanics!
Apparently, even more electrons can coexist in areas where the orbitals of the sets overlap.
What counter-intuitive mechanism allows even the "two’s company, three’s a
crowd" to become communal without any of them repelling any other? One
would expect the "atomic machinery" to be more orderly than this.
While adding "s" to "nlm" may have addressed the issue of
two electrons needing to occupy the same space, the fact that two or more
orbitals of the same "n-level" occupied much of the same space either escaped
notice or has simply been ignored. One would hope that the former has been the case.
However, it is hard to believe that the issue has not arisen often during the entire century that has
just passed; especially the last fifty! The spdf/nlms model has been presented as
THE proper mathematical representation of the quantum mechanical atomic theory. Fifty
years ago, the theory was still a theory. To my knowledge, it has not become a
physical law, yet. A model that requires
different electrostatic physical laws than those actually observed, that has several mathematical solutions
of which only one is endorsed, that reduces the number of orbitals from 6 to 5
when the mathematics gives one too many, and that ignores common space overlap
of orbitals is hardly the gem it is made out to be. Apparently, the hard
sciences are willing to make an exception for the most
"Nobel-garnering" of theoretical models.
Conclusion:
the spdf
orbital models look neat and crisp when viewed as independent sets of orbitals, but become a
garbled mess when combined beyond the simplest grouping of 8. This garbled mess
becomes even worse as more periods are considered. The spdf model is simply a
rigid orbital, “file cabinet” model, starting with a single drawer and
stacking more on top. The spdf model is rather myopic when broad
application is considered. Dogged adherence to its rigidity indicates that
either little
has been learned in the past century about the actual structure or that no one
dares to disturb the sacred icon.
Caveat: lest the reader believe that I think very poorly of those scientists that developed the spdf/nlns model,
let me assure you that I have great admiration for their reasoning
and experimental efforts. The level of today's science is what it is because of
their efforts and those of many, many others. It is attention to the continued adoration of a physical law-defying
model to the exclusion and suppression of non-physical law-defying explanations that I
give voice.
Think about alternative
models that do not need the spdf assumptions

Consider, for example, the logic of
starting from the standpoint of accommodating all of the electrons of each
period in a symmetrical manner AND then seeing what subsets they contain. The
MCAS model was developed with just this approach. The figure below shows how the
MCAS model accommodates the differing numbers of electrons needed for each
layer.
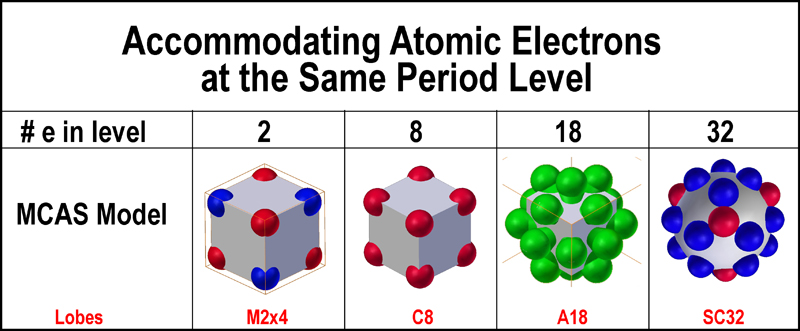
Nesting
of the orbital types is clearly evident with each electron having a
“dedicated” home abode. Sub-orbital units can be established to associate
electrons into groups as required (that is demonstrated for the 2 electron
case), but an overall symmetrical distribution of electron density (as defined
by the lobes) must be maintained. The complete nesting symmetry of all of the
MCAS orbital types is shown in the figure at the right. A full complement of
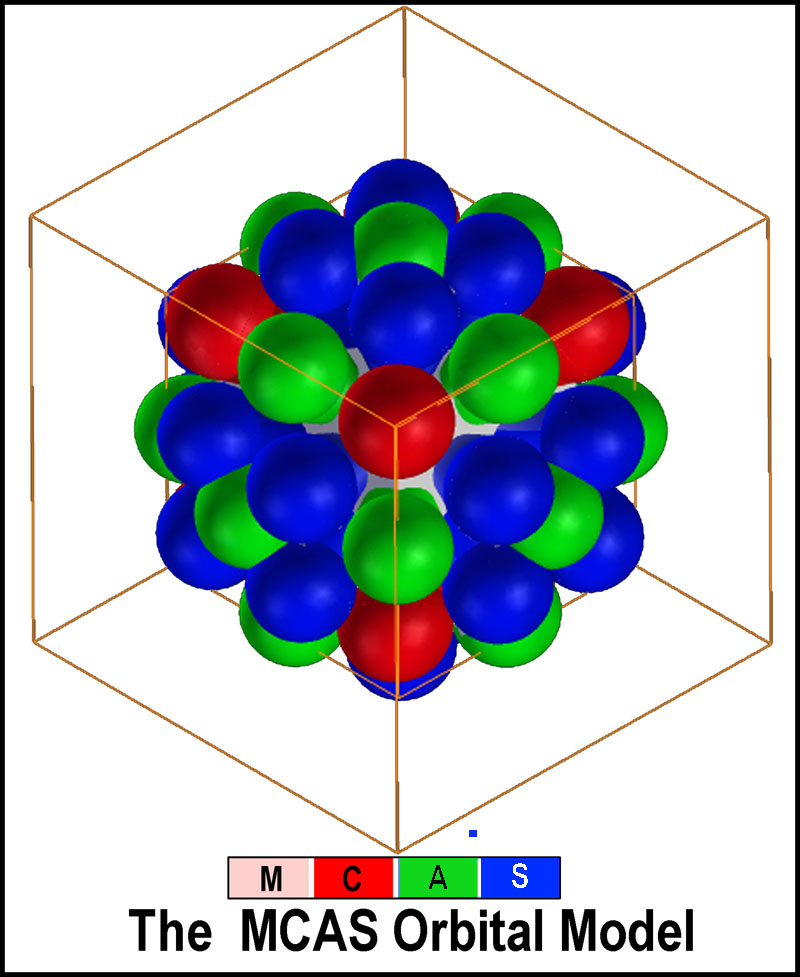
nested orbitals possible at the same n-level is 50 (8C + 18A +24S).
Layer nesting of orbitals is not
a feature of the spdf model! Nor does it provide dedicated (orthogonal) space of
the orbital sets as touted. The following figure provides a side-by-side
comparison of how the spdf and MCAS models handle the 2, 8, 18, 32 electrons around an
atom to provide an easier recognition of their differences.
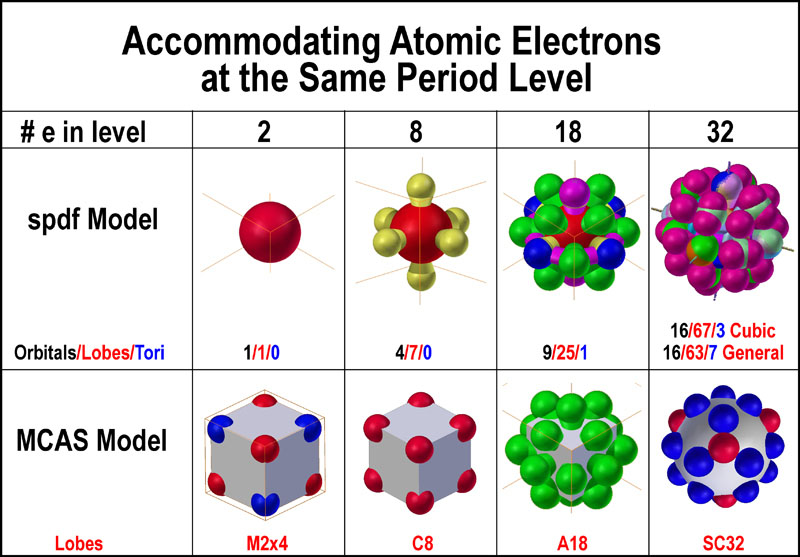
So, what is so important about
“nesting”? Consider that the currently known elements require seven (7)
periods (layers) of electrons. The last element in the 7th period will
contain 118 electrons in periods of 2, 8, 18, 32, 32, 18, and 8 electrons.
These layers are not onion-skin layers independent of the layer above and
below. “Nesting” provides the
mechanism that allows electron orbitals to be placed in each layer in a manner
that provides the lowest energy for the total arrangement. “Nesting” of the
orbitals is clearly seen in the orbital structure of the noble gases when modeling has been performed with MCAS
orbitals (see figure
below; its generation is presented elsewhere[6]
- click
here to connect). Note that only two levels of A or S sets ever
need coordinating!
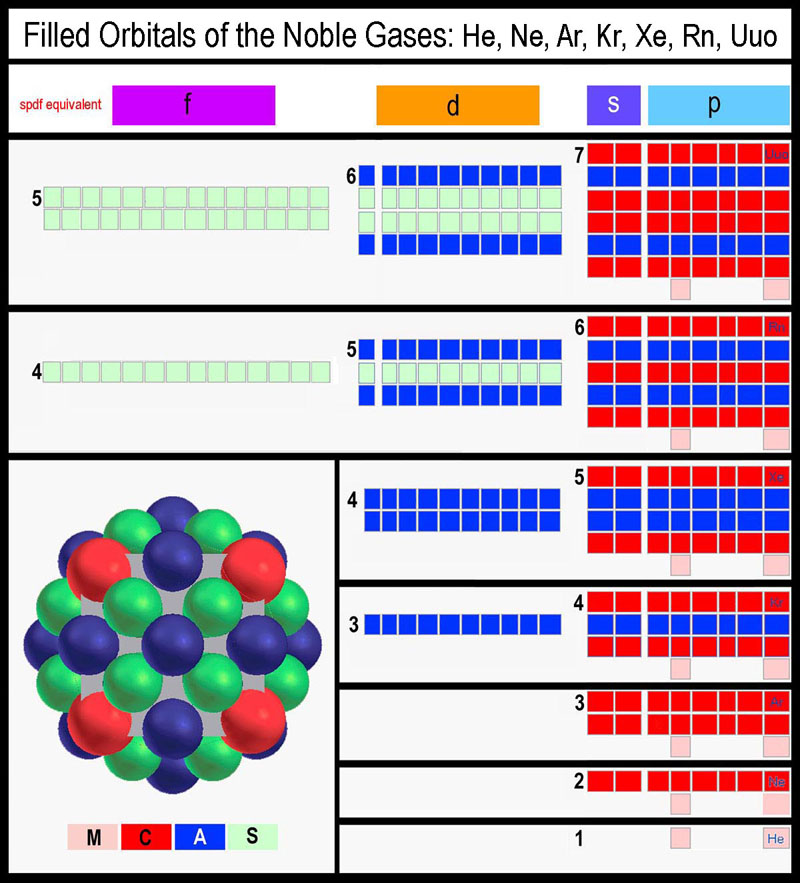
Electrons in similar orbital types of different “periodic
levels” are coordinated as orbital dimensions range from the nucleus outward
to the farthemost extent of the orbital type. Dynamic coordination is an
inherent feature of the MCAS model.
SUMMARY
The spdf model is a stoic mathematical model that is based on creating
independent sets of orbitals containing 1, 3, 5 and 7 pairs of electrons. The
resulting sets have memorable 3D images of their individual components.
Individually, each set is aligned along the x, y, and z axes. When combined to
handle 2, 8, 18, and 32 electrons in 1, 4, 9, 16 pairs, these sets are not
orthogonal to one another and overlap from the very start. The noble elements
represent very well-coordinated groups of 2, 8, 18, and 32 electrons. When the
spdf orbitals are subjected to a 3D, visual summing, they present anything but a
neat assemblage of the electron spaces needed to handle the required number of
“periodic” electrons. It is not a matter of how the spdf orbital sets have
been generated (the mathematical logic can be clearly followed and taught), but
whether the summation logic follows the same constraints that are applied to the
individual sets. When the orbital sets are combined, it is clear that the same
constraints are not followed.
In contrast to the spdf electron
orbital model, the MCAS electron orbital model provides simple, nesting,
configurations to handle the electrons needed for the periods of the periodic
table of elements.
“Comparing the Logic behind the spdf and MCAS Models” also
addresses the spd portion of the spdf model[7]
- click here to
connect.
ADDENDUM
The following figure is given to aid in understanding the
MC “mirrored” orbital concept.
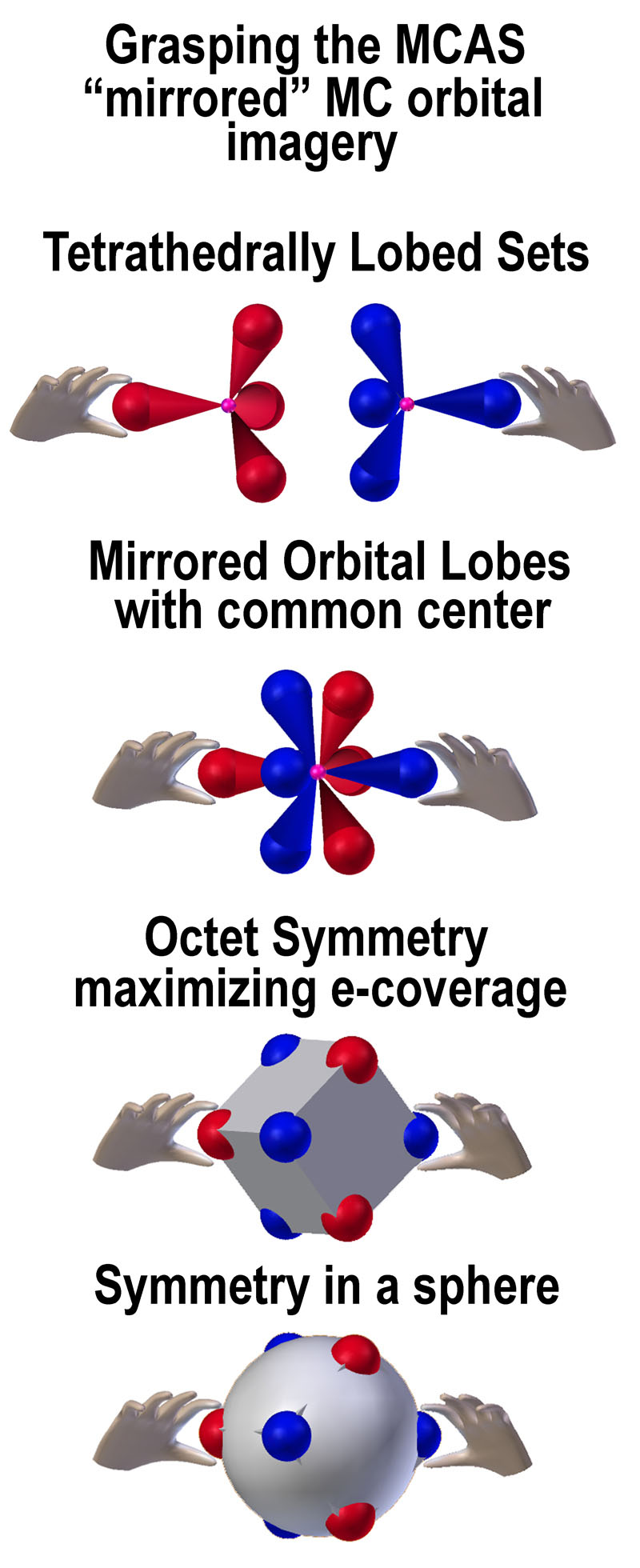
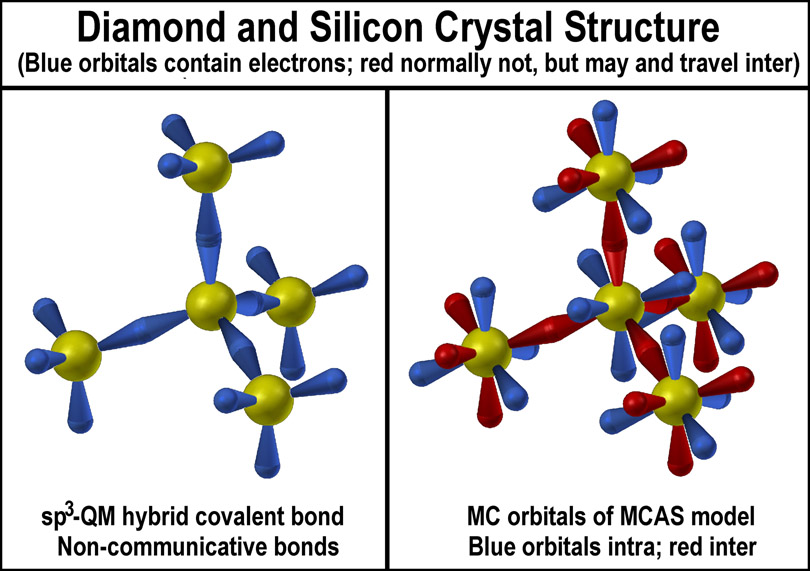
 Stanch
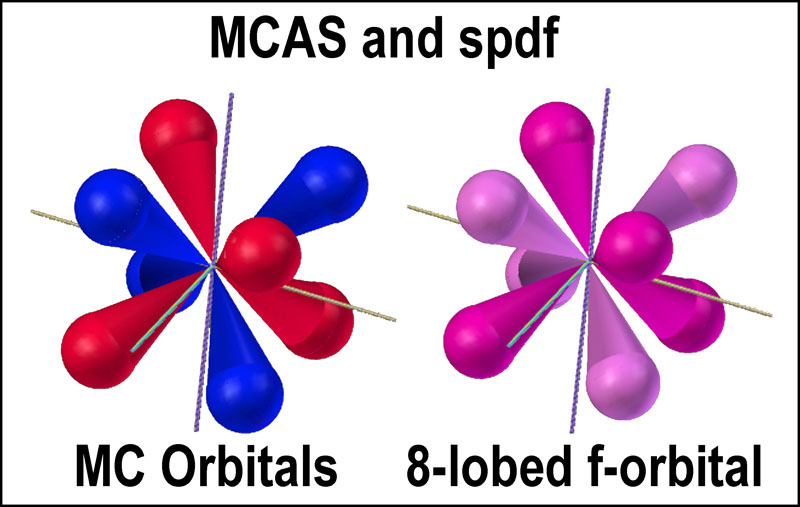
adherents to the spdf model who thus oppose tetrahedral orbitals in place of
the spherical one should consider the similarity of one of their f-orbitals to
the MC pair (see figure at right). Two electrons can occupy the f-orbital, but
just how one or two of them can occupy those 8 lobes is not clear. How they do
so in the MC orbitals is.
Stanch
adherents to the spdf model who thus oppose tetrahedral orbitals in place of
the spherical one should consider the similarity of one of their f-orbitals to
the MC pair (see figure at right). Two electrons can occupy the f-orbital, but
just how one or two of them can occupy those 8 lobes is not clear. How they do
so in the MC orbitals is.
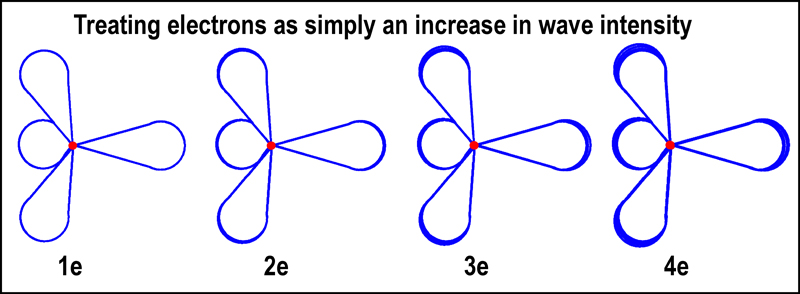
For adherents of the wave approach to
electrons, think of the edges of the lobes of the
tetrahedral orbital as defining the wave length. The number of electrons in the
tetrahedral orbital can be thought of as the wave’s intensity. This imagery is
presented in the figure below. The size of the tetrahedral lobes determine how
many electrons can be accommodated. The first tetrahedral unit is only large
enough to handle a single electron. The wave intensity of a single tetrahedral
orbital unit beyond that first level can scale to 4 (1 per lobe); the sum of the two mirrored
tetrahedral orbitals can reach 8.
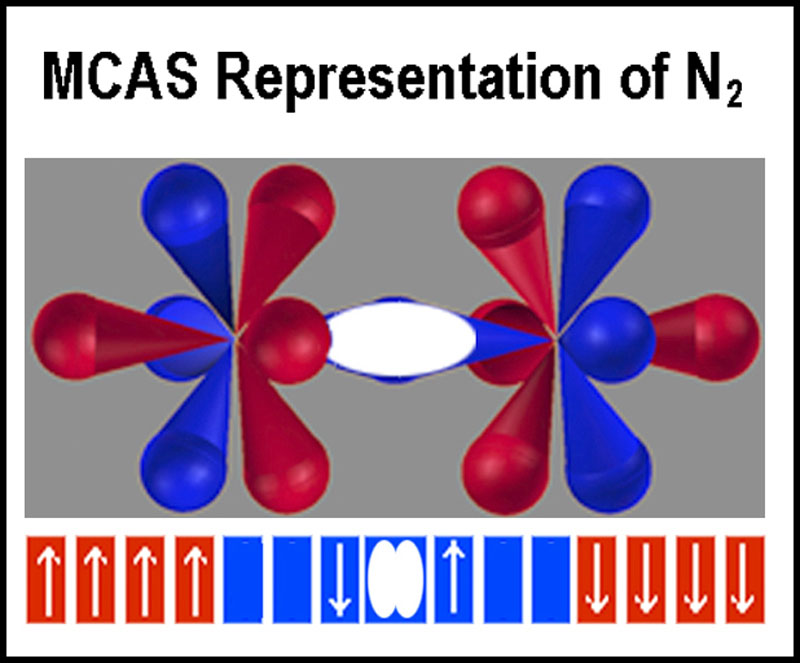 Bonding
using the orbitals of the MCAS model has been presented elsewhere where
electrostatic attracting and repelling of the electrons and nuclei are included[8].
The nitrogen molecule is shown at the right.
Bonding
using the orbitals of the MCAS model has been presented elsewhere where
electrostatic attracting and repelling of the electrons and nuclei are included[8].
The nitrogen molecule is shown at the right.
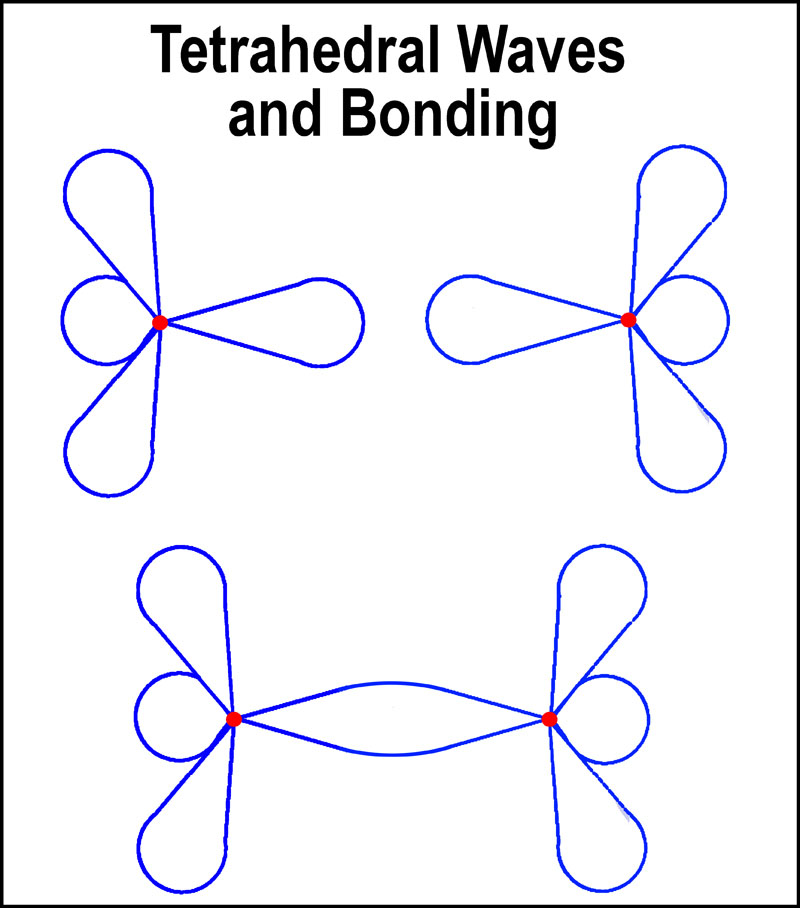 In
keeping with the wave imagery above, the figure at the right shows the
combination of tetrahedral waves from two separate atoms. Lower energy results
from the longer (~doubled!) combined wave length. At the lowest orbital level, this
would be one of the possibilities for H2 (2
electrons)[8]. For the next level and a larger tetrahedral unit,
the combined wave can accommodate up to 6 electrons (F2). A 7th electron
will not be accommodated as the combined wave would be more energetic than the
two individual ones. Also, a “permanent” electron presence would occur
between the nuclei. Think about Ne and F not forming a bond.
In
keeping with the wave imagery above, the figure at the right shows the
combination of tetrahedral waves from two separate atoms. Lower energy results
from the longer (~doubled!) combined wave length. At the lowest orbital level, this
would be one of the possibilities for H2 (2
electrons)[8]. For the next level and a larger tetrahedral unit,
the combined wave can accommodate up to 6 electrons (F2). A 7th electron
will not be accommodated as the combined wave would be more energetic than the
two individual ones. Also, a “permanent” electron presence would occur
between the nuclei. Think about Ne and F not forming a bond.
For those preferring a particulate model,
the combined “wave lines” indicate coordinated passage of electrons around
each nucleus and then onto the other giving greater mean coverage to the nuclei.
There are electrostatic interactions of
these orbitals with the other tetrahedral orbitals that are not shown here.
For those preferring a probability model,
the overlapped orbitals are simply a way of reducing the total orbital volume to
be filled with the totality of electron density; 8 orbitals reduced to 7. A high
concentration of electron negativity should NOT be expected in the overlap,
however, as the other lobes have requirements, too. For N2, 2
electrons would be distributed among the 7 and, as a first approximation, the
overlapped region would have 0.29 of an electron; not 2. For F2, it
would have 0.87 of an electron.
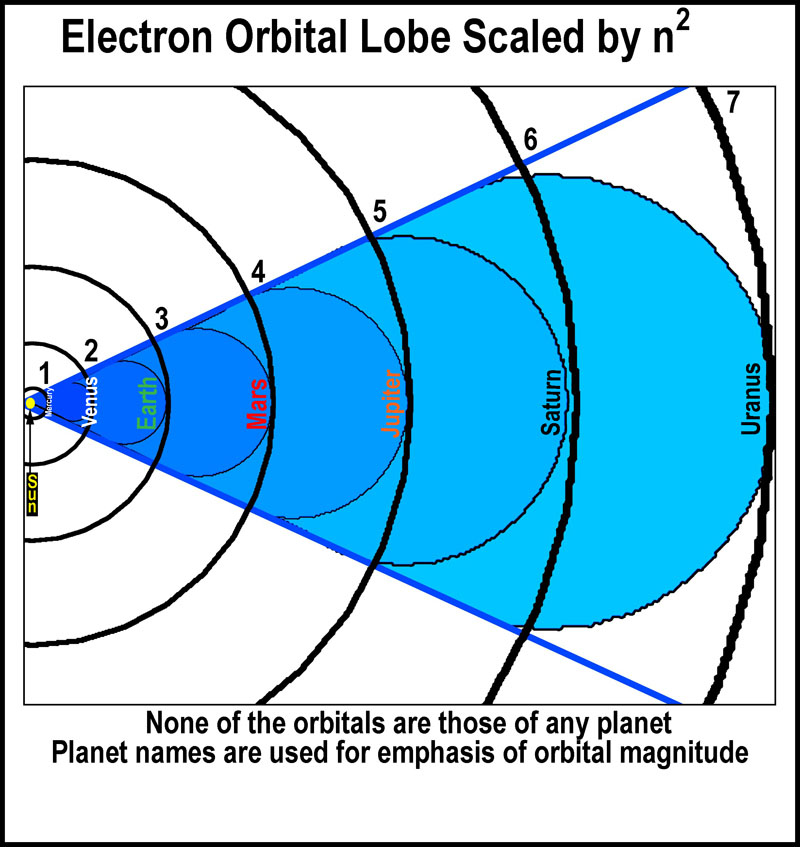 Orbitals
scale by n2 (see the figure at the right). It is easy to see how a
wave or moving particle could create such orbital spaces as they relate to
defined energy levels. It takes a lot of energy to reach the outer limits.
With sufficient energy an electron will escape the nuclear grip and leave a
positively charge atom (ion). Otherwise, the electron remains associated with
the nucleus in a controlled
manner.
Orbitals
scale by n2 (see the figure at the right). It is easy to see how a
wave or moving particle could create such orbital spaces as they relate to
defined energy levels. It takes a lot of energy to reach the outer limits.
With sufficient energy an electron will escape the nuclear grip and leave a
positively charge atom (ion). Otherwise, the electron remains associated with
the nucleus in a controlled
manner.
The definition of orbital space by electron
probability (defined as the likelihood of finding an electron in a given spot)
is less facile. Since the spdf model has electron densities concentrated in
overlapped orbital spaces along the x, y, and z axes, what keeps the electrons
in those overlapped probability clouds confined to a particular orbital?
Probability information reads like a census of the
number of
residents in tenement buildings of a complex without explaining why or how those
residents got there. When thinking about forming bonds by overlapping e-rich
orbitals - as is the current approach, consider the effect of stuffing more
residents, especially hot-heads, into the same tenement space while leaving
other space vacant.
REFERENCES
[8]
a) Understanding the Bonding of Second Period Diatomic Molecules (spdf vs
MCAS), Joel Mann Williams - http://gsjournal.net/Science-Journals/Essays/View/4850;
b) Comparing Several Orbital Approaches to the Hydrogen, Joel Mann Williams - http://gsjournal.net/Science-Journals/Essays/View/4885;
c) Electronic Bonding of Atoms, Joel Mann Williams - http://gsjournal.net/Science-Journals/Essays/View/4043;
d) Modeling the MCAS Way, Joel M Williams - http://arxiv.org/html/physics/9902046v2
(sharper imagery at http://pages.swcp.com/~jmw-mcw/science)

 _
_![]()
.jpg)
![]()
![]()






 dedicated
to the
preceding one. This is seen in the center column of the above figure and
emphasized in the figure at the right. Roughly, the electron density of ~6
electrons, out of 32, is concentrated along this axis. With similar overlaps
along the x and y axes, ~60% of the total electron density of a period is
concentrated in ~20% of the spherical volume! This may be nice for mathematics,
but it is unlikely to occur in a real world situation.
dedicated
to the
preceding one. This is seen in the center column of the above figure and
emphasized in the figure at the right. Roughly, the electron density of ~6
electrons, out of 32, is concentrated along this axis. With similar overlaps
along the x and y axes, ~60% of the total electron density of a period is
concentrated in ~20% of the spherical volume! This may be nice for mathematics,
but it is unlikely to occur in a real world situation.






 Stanch
adherents to the spdf model who thus oppose tetrahedral orbitals in place of
the spherical one should consider the similarity of one of their f-orbitals to
the MC pair (see figure at right). Two electrons can occupy the f-orbital, but
just how one or two of them can occupy those 8 lobes is not clear. How they do
so in the MC orbitals is.
Stanch
adherents to the spdf model who thus oppose tetrahedral orbitals in place of
the spherical one should consider the similarity of one of their f-orbitals to
the MC pair (see figure at right). Two electrons can occupy the f-orbital, but
just how one or two of them can occupy those 8 lobes is not clear. How they do
so in the MC orbitals is.
 Bonding
using the orbitals of the MCAS model has been presented elsewhere where
electrostatic attracting and repelling of the electrons and nuclei are included
Bonding
using the orbitals of the MCAS model has been presented elsewhere where
electrostatic attracting and repelling of the electrons and nuclei are included In
keeping with the wave imagery above, the figure at the right shows the
combination of tetrahedral waves from two separate atoms. Lower energy results
from the longer (~doubled!) combined wave length. At the lowest orbital level, this
In
keeping with the wave imagery above, the figure at the right shows the
combination of tetrahedral waves from two separate atoms. Lower energy results
from the longer (~doubled!) combined wave length. At the lowest orbital level, this
 Orbitals
scale by n2 (see the figure at the right). It is easy to see how a
wave or moving particle could create such orbital spaces as they relate to
defined energy levels. It takes a lot of energy to reach the outer limits.
With sufficient energy an electron will escape the nuclear grip and leave a
positively charge atom (ion). Otherwise, the electron remains associated with
the nucleus in a controlled
manner.
Orbitals
scale by n2 (see the figure at the right). It is easy to see how a
wave or moving particle could create such orbital spaces as they relate to
defined energy levels. It takes a lot of energy to reach the outer limits.
With sufficient energy an electron will escape the nuclear grip and leave a
positively charge atom (ion). Otherwise, the electron remains associated with
the nucleus in a controlled
manner.