Abstract
The current spdf and MO modeling of
chemical molecules
are well-established, but do so by continuing to assume
that non-classical physics is operating. The MCAS electron orbital model is an
alternate particulate model based on classical physics. This paper describes
its application to the diatomic molecules of the second period of the periodic
table. In doing so, it addresses their molecular electrostatics, bond
strengths, and electron affinities. Particular attention is given to the
anomalies of the carbon diatom. Questions are raised about the sensibleness of
the spdf model’s spatial ability to contain two electrons on an axis between
diatoms and its ability to form π-bonds from parallel p-orbitals located
over the nuclei of each atom. Nitrogen,
carbon monoxide, oxygen, and fluorine all have the same
inter-nuclei bonding: all “triple bonds” of varying strength caused by
different numbers of
anti-bonding electrons.
The spdf model was devised for single atoms by physicists and mathematicians.
Kowtowing to them, chemists produce hybrid orbitals to explain how atoms could
actually form molecules. Drawing
these hybrids and meshing them on paper might look great, but, constrained to
measured interatomic physical dimensions and electrostatic interactions, bonding
based on the spdf-hybrids (sp, sp2, sp3) is illogical. To have even one electron
occupy the “bond” region between the nuclei of diatomic molecules, at the
expense of reduced coverage elsewhere, does not make sense for stable molecules.
To have two repelling electrons in the area is nonsensical. To a third object,
the perceived influence of two electrons may be additive, but the influence
perceived by those two electrons of each other will hardly be congenial or
neutral, as implied in the “duality” concept! While some question whether
electrons are particulate, I have chosen to accept the fact that electrons have
mass and, if the mass is a string, for example, it must at least be a ball of
twine when fired at something. My qualms have to do with the spdf model and the
history of forcing it to “meet” the experimental with mathematics ruling
over common application of physical limitations, like e-e repulsion, and
chemical properties, like the position of hydrogen in the periodic table. The
MCAS model for bonding that is discussed below easily explains why hydrogen has
the characteristics of carbon and thus belongs over carbon in the familiar
periodic table.
This article is about bonding in simple diatomic molecules, however.
%20and%20C%20(MCAS)%20Orbitals.jpg) The
MCAS model will be used to inspect the bonding interactions of simple diatomic
molecules. The second period diatomic molecules use just the sp orbitals of the
currently accepted spdf model or the M/C orbitals of the MCAS model.
The image to the right is an artistic rendition of how the two models place the
electron orbitals about the atoms. The spdf model has 7 lobes for an eventual 8
electrons, thus, the requirement to “pair” electrons in the “red”
s-orbital – achieved mathematically by spin-reversal. The 8 lobes of the MCAS
model easily accommodated 8 electrons with “pairing” by reciprocal motion.
For Neon, its 8, second period, electrons are not all uniformly packed around
the nucleus with the spdf model. With the MCAS model, they are. Note that for
equal orbital extent, the spdf model uses 5.2x the cubic volume of the MCAS
model; i.e., the spdf model is not compact as one might expect the electron
structure around a nucleus to be. For the purposes of forming diatomic molecules
of the second period, the spdf model must be modified to sp, sp2, or
sp3 hybrids although some MO treatments just make bond-antibond
lattices without prehybridizing. No such hybridization is needed with the MCAS
model. Since hybridized spdf modeling is so extensively taught in all levels of
chemistry text, the reader is assumed to be well acquainted with them.
The
MCAS model will be used to inspect the bonding interactions of simple diatomic
molecules. The second period diatomic molecules use just the sp orbitals of the
currently accepted spdf model or the M/C orbitals of the MCAS model.
The image to the right is an artistic rendition of how the two models place the
electron orbitals about the atoms. The spdf model has 7 lobes for an eventual 8
electrons, thus, the requirement to “pair” electrons in the “red”
s-orbital – achieved mathematically by spin-reversal. The 8 lobes of the MCAS
model easily accommodated 8 electrons with “pairing” by reciprocal motion.
For Neon, its 8, second period, electrons are not all uniformly packed around
the nucleus with the spdf model. With the MCAS model, they are. Note that for
equal orbital extent, the spdf model uses 5.2x the cubic volume of the MCAS
model; i.e., the spdf model is not compact as one might expect the electron
structure around a nucleus to be. For the purposes of forming diatomic molecules
of the second period, the spdf model must be modified to sp, sp2, or
sp3 hybrids although some MO treatments just make bond-antibond
lattices without prehybridizing. No such hybridization is needed with the MCAS
model. Since hybridized spdf modeling is so extensively taught in all levels of
chemistry text, the reader is assumed to be well acquainted with them.
Atoms of the second period elements cover 8 positions with electrons as they are
available. The following figure shows 2 MCAS-model nuclei placed on an axis in
close proximity to one another.
.jpg)
Consider a case wherein 8 electrons fill the 8 lobes; such as with a fluoride
ion. With all of the orbital lobes filled, the nucleus is symmetrically
surrounded with “guarding” electrons. Consequently, it has no unguarded
“posts” that need protecting. On the other hand, fluorine atoms have only 7
electrons. So, how can the unguarded “post” (see small “?’s” in the
above figure) be protected? Without an available “free electron”, another
atom with a similar deficiency participates. The deficiencies merge and a bond
is born. There is neither a need to spin-reverse an electron nor to ignore
electron-electron repulsion as occurs in the mathematical treatment of the
current spdf-hybrid modeling. In the way the orbitals are arranged in this
paper, the red ones are “bonding” and the blue ones are “antibonding”.
Note that the bonding quartets include the exo-positions.
.jpg) The
figure at the right illustrates the situation with accompanying electrostatic
interactions. The electrostatic contours were determined with the nuclei at
their experimental distance apart and with the electrons at the orbital
extremes. Non-bonding electron charge was distributed uniformly to each lobe.
Classical electrostatic attractions and repulsions with were used. The
electrostatic images clearly demonstrate the surrounding symmetry of the
8-electron fluoride ion. They also demonstrate the weakness of the bond in the
fluorine molecule. There is little negativeness (blue in the figure) protecting
the molecule in this area. Consequently, fluorine is a very reactive
electron-acceptor. Thus, while “neighboring” atoms may join to lower their
individual vulnerabilities, this is inferior to having a full-time electron do
the job. The current practice of putting electrons between the nuclei at the
expense of de-shielding in other areas may be mathematically attractive, but it
is illogical from standard electrostatic interactions. That is why physics had
to be different at the atomic level. A bond represents electron-deficiency NOT
electron-abundance. Orbital overlap may, however, provide a conduit for
transient flow (!) of electrons from the antibonding quartet of one atom to
another.
The
figure at the right illustrates the situation with accompanying electrostatic
interactions. The electrostatic contours were determined with the nuclei at
their experimental distance apart and with the electrons at the orbital
extremes. Non-bonding electron charge was distributed uniformly to each lobe.
Classical electrostatic attractions and repulsions with were used. The
electrostatic images clearly demonstrate the surrounding symmetry of the
8-electron fluoride ion. They also demonstrate the weakness of the bond in the
fluorine molecule. There is little negativeness (blue in the figure) protecting
the molecule in this area. Consequently, fluorine is a very reactive
electron-acceptor. Thus, while “neighboring” atoms may join to lower their
individual vulnerabilities, this is inferior to having a full-time electron do
the job. The current practice of putting electrons between the nuclei at the
expense of de-shielding in other areas may be mathematically attractive, but it
is illogical from standard electrostatic interactions. That is why physics had
to be different at the atomic level. A bond represents electron-deficiency NOT
electron-abundance. Orbital overlap may, however, provide a conduit for
transient flow (!) of electrons from the antibonding quartet of one atom to
another.
.jpg) Consider
now the bonding in some simple diatom molecules as given by the MCAS model. The
figure at the right shows a plot of the experimental bond strength
of the diatomic molecules of the second period of the periodic table.
Li-Li has a modest bond strength with a single “bonding” electron on
each atom and no antibonding. There is an “antibonding” electron on each Be
atom (this gives symmetry to the individual atom). The greater nuclear positive
charge attractions for the bonding electrons is countered by greater nuclei
repulsion and repelling of the opposite nucleus’ antibonding electron by the
nucleus’ bonding electron and the bond is weaker. As nuclear charges increase
and more “bonding” electrons surround the nuclei, bond strength increases
greatly (note green line). Maximum bond strength is obtained when there are
maximum “bonding” electrons and minimum “antibonding” electrons. This
occurs with nitrogen. Beyond nitrogen, “antibonding” electrons are added.
Increasing interatomic “bonding-antibonding electron repulsion” and
increasing repulsion of the nuclei overshadow increasing nucleus-bonding
electron attractions. The MCAS model demonstrates the observed results without
altering the disposition of the electrons around the nuclei. Contrast this with
the ever changing hybridization required for the spdf-model to do the same.
Consider
now the bonding in some simple diatom molecules as given by the MCAS model. The
figure at the right shows a plot of the experimental bond strength
of the diatomic molecules of the second period of the periodic table.
Li-Li has a modest bond strength with a single “bonding” electron on
each atom and no antibonding. There is an “antibonding” electron on each Be
atom (this gives symmetry to the individual atom). The greater nuclear positive
charge attractions for the bonding electrons is countered by greater nuclei
repulsion and repelling of the opposite nucleus’ antibonding electron by the
nucleus’ bonding electron and the bond is weaker. As nuclear charges increase
and more “bonding” electrons surround the nuclei, bond strength increases
greatly (note green line). Maximum bond strength is obtained when there are
maximum “bonding” electrons and minimum “antibonding” electrons. This
occurs with nitrogen. Beyond nitrogen, “antibonding” electrons are added.
Increasing interatomic “bonding-antibonding electron repulsion” and
increasing repulsion of the nuclei overshadow increasing nucleus-bonding
electron attractions. The MCAS model demonstrates the observed results without
altering the disposition of the electrons around the nuclei. Contrast this with
the ever changing hybridization required for the spdf-model to do the same.
.jpg) The
1st ionization potential of a single atom is now addressed. The
figure at the right shows the experimental data
of the second period elements. Ionization potential is the difference in the
energy level of the original state and that of the generated state. The green
line indicates ionization from “optimal” bonding-antibonding electron
configurations (Be, N, and Ne; all green arrows) to “less optimal”
configurations. Red arrows indicate electrons in “non-optimal”
configurations. For Li, B, and O, their removal gives an “optimal”
configuration. For C and F, removal of an electron from a “non-optimal”
configuration just gives another “non-optimal” one. The N-value is slightly
lower than expected.
The
1st ionization potential of a single atom is now addressed. The
figure at the right shows the experimental data
of the second period elements. Ionization potential is the difference in the
energy level of the original state and that of the generated state. The green
line indicates ionization from “optimal” bonding-antibonding electron
configurations (Be, N, and Ne; all green arrows) to “less optimal”
configurations. Red arrows indicate electrons in “non-optimal”
configurations. For Li, B, and O, their removal gives an “optimal”
configuration. For C and F, removal of an electron from a “non-optimal”
configuration just gives another “non-optimal” one. The N-value is slightly
lower than expected.
.jpg) The
electron affinity of a single atom and its diatomic molecule is now addressed.
The figure at the right shows the experimental data
of the second period elements. Consider first the single atom e-affinities
(yellow squares and accompanying single dual 4-lobe C-orbitals). Li has an
affinity to add an electron to provide symmetry. Adding one to Be destroys its
inherent symmetry. Increased nuclear charge and improved symmetry occur with B
and C. Adding an electron to N destroys its symmetry which counters its higher
nuclear charge. Improved symmetry occurs again with O and F with increased
nuclear charge having a dramatic effect. For Ne, the 8-lobes are filled and,
consequently, there is no need for an additional electron at this level.
The
electron affinity of a single atom and its diatomic molecule is now addressed.
The figure at the right shows the experimental data
of the second period elements. Consider first the single atom e-affinities
(yellow squares and accompanying single dual 4-lobe C-orbitals). Li has an
affinity to add an electron to provide symmetry. Adding one to Be destroys its
inherent symmetry. Increased nuclear charge and improved symmetry occur with B
and C. Adding an electron to N destroys its symmetry which counters its higher
nuclear charge. Improved symmetry occurs again with O and F with increased
nuclear charge having a dramatic effect. For Ne, the 8-lobes are filled and,
consequently, there is no need for an additional electron at this level.
The electron affinity of the diatomic molecules is a bit different (red circle
and overlapped C-orbitals in the preceding figure). Li-Li has a slightly lower
e-affinity than Li as the addition of an electron to the antibonding lobes would
destabilize the Li-Li bond. No data for Be-Be and B-B are given in the
reference. The C-C molecule has a much greater e-affinity than atomic C! The N-N
molecule would not be expected to have much of a difference in e-affinity than
the corresponding single atom which has none. The O-O molecule has a much lower
e-affinity than a single O atom. Similarly, the F-F molecule has a lower one
than the F atom, but not much lower.
.jpg) The
reason for the deviant electron affinities of the diatomic molecules becomes
clear when the electrostatic interactions are considered, especially the
enormously greater e-affinity of C-C. The figure at the right shows the
calculated positive and negative charge levels around the molecules in the MCAS
style with electrons at maximum orbital extension.
The
reason for the deviant electron affinities of the diatomic molecules becomes
clear when the electrostatic interactions are considered, especially the
enormously greater e-affinity of C-C. The figure at the right shows the
calculated positive and negative charge levels around the molecules in the MCAS
style with electrons at maximum orbital extension.
First, note that, as the nuclear
charge increases (C to Ne), the surround electrons become more tightly bound
(compact) and uniform, but always as symmetrical as possible.
Next, note the electrostatics of the diatomic molecules in the bonding area. The
images are for 6 bonding electrons between the nuclei; required for N2
to F2 as the bonding orbital quartets are filled. For C2,
it is only one of its options which is shown here to emphasize the molecule’s
great need for an exo-electron.
The nitrogen diatom is the most
uniformly bathed in negativeness. As nuclei-repulsion and interatomic
bonding-antibonding repulsions increase, the bond lengthens and bond energy
decreases. In the case of F2, the bond is greatly weakened, even with
the nuclei tugging on the opposite’s electrons. At Ne, the need for a bond is
replaced by an electron and the atom is more highly bathed in negativeness than
is the nitrogen molecule.
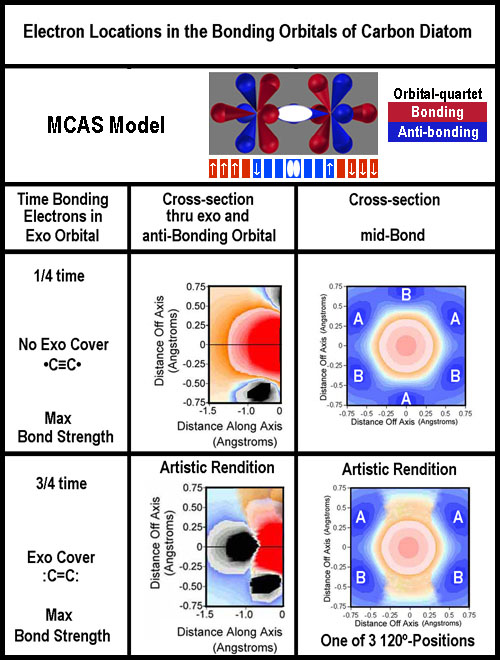 Valence
bond theory would require 4 bonds between the carbon nuclei to give 8 shared
– this was never taught that I remember; but apparently is getting some press[8].
The exo-deficient image above for
carbon is like •C≡C•
with just 7 electrons for each and the lone electrons anti-bonding, yet paired
(by opposite movement).
Valence
bond theory would require 4 bonds between the carbon nuclei to give 8 shared
– this was never taught that I remember; but apparently is getting some press[8].
The exo-deficient image above for
carbon is like •C≡C•
with just 7 electrons for each and the lone electrons anti-bonding, yet paired
(by opposite movement).
There are 2 MO versions: sp+2p version (3 bonds between the nuclei; equivalent
to the above: •C≡C•)
and s +3p version (2 bonds, thus :C=C:).[6]
One of the electrons outside the nuclei pair is in the non-bonding quartet; the
other is in the bonding quartet. They are not paired in the same orbital as is
usually implied. The MO model lumps the non-bonding together; here that is
clearly not the case.
Unlike the cases of N2,
O2, and F2, there are only 3 electrons to fill
the 4 bonding quartet lobes. They can be placed in 1 of 4 ways with 3 being
energetically equivalent. The two different options are shown in the figure to
the right.
Whether electrons are "paired" or not between the two nuclei will
depend on how they move in the bonding quartets.
Does the mid-bond cross-section
for the exo-covered option look like 2, side-by-side, A-B π-bonds for the
exo coverage? How about 3 A-B π-bonds for the “no exo cover” option?
Unlike the spdf/MO model, there is no connection; just proximity.
.jpg) Now
consider the carbon monoxide case. CO has the same number of electrons as does
nitrogen: 10. Unlike the case with nitrogen where each atom has the same number,
carbon has 4 and oxygen has 6. The figure at the right shows how the electrons
are redistributed when the CO molecule is formed. According to the MCAS
modeling, an electron from the “antibonding” orbital unit of oxygen is
transferred to the “bonding” orbital of carbon. This results in a permanent
dipole. With an electron arrangement like that of N2, CO should have
a bond strength attributed to a triple bond; actually it should be stronger
(experimentally observed) with the higher charge on oxygen tugging on the carbon
bonding electrons. I have included an MO description
of what is happening for comparison. The bonding and anti-bonding sigma and pi
orbitals/levels are easily formed schematically, if not envisioned physically.
Seems like the four 2s electrons form two exo non-bonding orbitals instead of a
sigma/anti-sigma pair! Since there are no unpaired electrons, MO requires (Hund’s
rule) that two electrons occupy each “bond” orbital. The MCAS model has no
such restriction as each orbital has a complementary opposite; thus, there are
no “unpaired” electrons, even if they are at opposite ends of the molecule.
Now
consider the carbon monoxide case. CO has the same number of electrons as does
nitrogen: 10. Unlike the case with nitrogen where each atom has the same number,
carbon has 4 and oxygen has 6. The figure at the right shows how the electrons
are redistributed when the CO molecule is formed. According to the MCAS
modeling, an electron from the “antibonding” orbital unit of oxygen is
transferred to the “bonding” orbital of carbon. This results in a permanent
dipole. With an electron arrangement like that of N2, CO should have
a bond strength attributed to a triple bond; actually it should be stronger
(experimentally observed) with the higher charge on oxygen tugging on the carbon
bonding electrons. I have included an MO description
of what is happening for comparison. The bonding and anti-bonding sigma and pi
orbitals/levels are easily formed schematically, if not envisioned physically.
Seems like the four 2s electrons form two exo non-bonding orbitals instead of a
sigma/anti-sigma pair! Since there are no unpaired electrons, MO requires (Hund’s
rule) that two electrons occupy each “bond” orbital. The MCAS model has no
such restriction as each orbital has a complementary opposite; thus, there are
no “unpaired” electrons, even if they are at opposite ends of the molecule.
Students can learn to follow the teaching and
textbook presentations of the spdf/MO model, but there are some serious
questions about these models. For example,
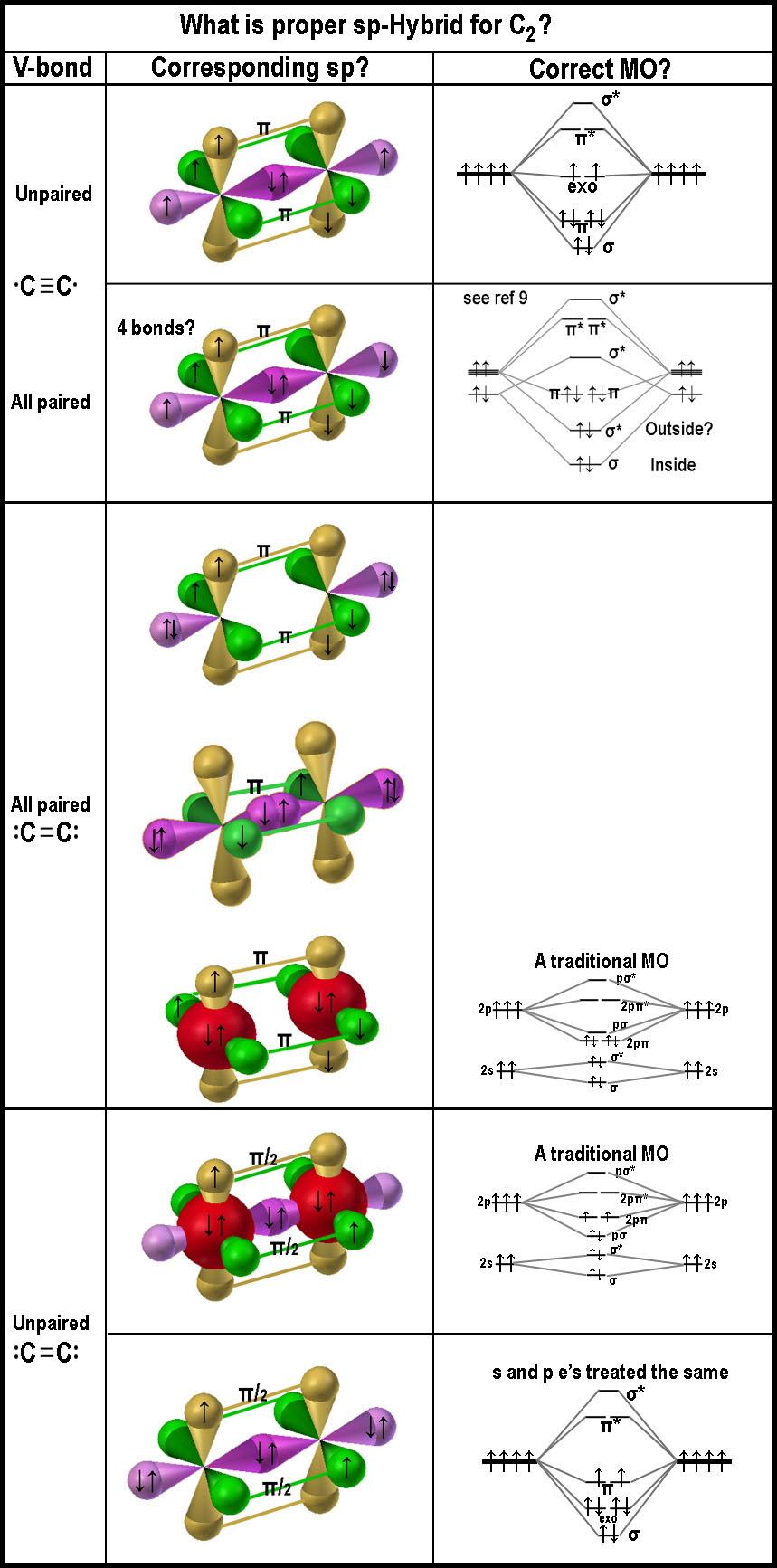 What is the
great driving force to make a C-C molecule have much larger e-affinity (~
equal to F atom) than a C-atom in the visual form of the spdf-model?
What is the
great driving force to make a C-C molecule have much larger e-affinity (~
equal to F atom) than a C-atom in the visual form of the spdf-model?
- Is there really enough space for two permanent
electrons in a sigma bond between the two nuclei, even if the electrons
could comingle as required in the mathematical treatment? If these electron
are located between the nuclei, as claimed in many models, why is there much
electrostatic negativity outside the internuclear region as is usually
illustrated in the hydrogen molecule case; esp. on the exo-nuclear
axis?
- Does the σ*-bond from the p-orbitals (as indicated in ref [9])
constitute a bond and thus giving rise to a 4th bond? It does cover the
molecule's ends. Having the two anti-bond lobes be a paired unit does get
around Hund! The MO also gets around the problems that arise with
the often used, very simplistic, boiler-plate, MO notations for C2.
These are illustrated in the bottom of the figure as "A
traditional MO"! One is left to wonder why C2
is so unstable when viewing the "4-bond" MO!
- Where
is the overlap that would even provide a π-bond? What make these
π-bonds strong? Some have proposed bent-bonds to provide overlap. Loops
might wor
 k
with reciprocal motion for pairing. Clouds
connecting the
tops and bottoms of the p-orbitals are also envisioned [9],
but what would create e-pairing. Overlap is not implied in simple spdf-modelings when nuclei are placed
apart and the p-orbitals are pear-shaped; spherical shaped p-orbital
lobes would be better, but that is not what the mathematicians decree to my
understanding. What keeps the electrons "floating"? MO modeling just indicates bonds and antibonds are formed without
regard to spatial requirements nor much in the way how other than
spin-pairing. What is a filled π-bond + a filled
anti-π-bond level but two, filled, non-bonding, p-orbitals – one
on each atom? What is a filled σ-bond + a filed anti-σ-bond
level but two, filled s-orbitals ala helium? What is the repulsion between these
filled non-bonding s and p-orbitals? Also, σ/σ* from an s-orbital
should definitely be different than σ/σ* from a p-orbital. Hence,
the need to have the p-orbitals form a 2-electron σ* MO in two separate
lobes at either end of the C-C axis [9] rather than
from the two 2-s orbitals. MOs that assume that sp-hybridization occurs
before bonding can get around this. Simply indicating that all the electrons
of each atom are the same and then placing them in the needed MOs as I have
done in several MO diagrams eliminates the problem. Of course, the real
problem is determining what MOs are needed rather than where the electrons
started. Carbon monoxide clearly demonstrated that electrons in a molecule
go where they are needed - just as they do in the atoms of the periodic
table [1].
k
with reciprocal motion for pairing. Clouds
connecting the
tops and bottoms of the p-orbitals are also envisioned [9],
but what would create e-pairing. Overlap is not implied in simple spdf-modelings when nuclei are placed
apart and the p-orbitals are pear-shaped; spherical shaped p-orbital
lobes would be better, but that is not what the mathematicians decree to my
understanding. What keeps the electrons "floating"? MO modeling just indicates bonds and antibonds are formed without
regard to spatial requirements nor much in the way how other than
spin-pairing. What is a filled π-bond + a filled
anti-π-bond level but two, filled, non-bonding, p-orbitals – one
on each atom? What is a filled σ-bond + a filed anti-σ-bond
level but two, filled s-orbitals ala helium? What is the repulsion between these
filled non-bonding s and p-orbitals? Also, σ/σ* from an s-orbital
should definitely be different than σ/σ* from a p-orbital. Hence,
the need to have the p-orbitals form a 2-electron σ* MO in two separate
lobes at either end of the C-C axis [9] rather than
from the two 2-s orbitals. MOs that assume that sp-hybridization occurs
before bonding can get around this. Simply indicating that all the electrons
of each atom are the same and then placing them in the needed MOs as I have
done in several MO diagrams eliminates the problem. Of course, the real
problem is determining what MOs are needed rather than where the electrons
started. Carbon monoxide clearly demonstrated that electrons in a molecule
go where they are needed - just as they do in the atoms of the periodic
table [1].
- C2 should have two unpaired electrons in the triple bond
case (•C≡C•),
if Hund’s rule is to be obeyed in the current models; like the top figure on the right? Is the
no-sigma bond image logical, as near the bottom of the figure on the right, if there
are paired electrons in the exo-bonds, as indicated in the double bond case
(:C=C:), which has
no unpaired electrons? Or are there two empty p-orbitals with one sigma bond
and one π-bond? The filled s-orbital spheres (red) near the bottom are more in line with
"traditionally presented MO diagrams". If they look a bit strange,
one might consider that the "simple 'serves-all' MO approach" does
not serve all! This "red sphere" illustration of anti-bonding
negating bonding to yield s-orbitals emphasizes the shortcomings of the
simple MO treatment. Shown this way, the 3D imagery clearly indicates that
the 2-s orbitals are not involved in the bonding process in accordance with
the accompanying MO diagram. The bottom MO might make sense, if, in fact, p-orbitals can form π-bonds;
especially 1-electron π-bonds! The reader is sure to find some
others. No wonder some teachers might want to forget the Bohr-orb
descendants. Of course, some of the learned might want something more
tangible than some energy level lines on paper. I did as I tried to
understand chemical reaction mechanisms, etc.
- 3-D images of the bonding and antibonding orbitals
should be presented for students to grasp what is being presented in the MO
diagrams. The figure above right does not show antibonding sigma and anti-π-bonds.
MO for C2 has an anti-sigma. Where? Seems a lot of extra stuff to
explain what is going on, when the MCAS approach does it so uncomplicatedly.
 The
figure at the right presents conceptual imagery of the Valence-Bond (VB),
Molecular Orbital (MO) and MCAS approaches to the hydrogen molecule. This allows
the three to be compared in the simplest molecular case.
The
figure at the right presents conceptual imagery of the Valence-Bond (VB),
Molecular Orbital (MO) and MCAS approaches to the hydrogen molecule. This allows
the three to be compared in the simplest molecular case.
The discussion
has being moved to a separate location. Click here.
Serious consideration of spatial placements and e-e repulsions should raise
major concerns, indeed, about the spdf-hybrid system and its MO offshoot. The MCAS model, on the
other hand, provides a physical representation that does not resort to e-e
non-repelling couplets and stresses coverage of the nuclei on all fronts, rears,
and sides.
Summary
The MCAS electron orbital model
provides a compact orbital arrangement which explains bond strength, 1st
ionization potential, and electron affinity behavior of the diatomic molecules
of the second period of the periodic table. It does so without hybridizing
(reconfiguring) the orbitals as the spdf model is required to do. It does so
while obeying classical physics; something the spdf approach has to declare
invalid to operate. Hence, the MCAS model demonstrates that classical physics
operates down to and includes the electron orbitals nanospace.




%20and%20C%20(MCAS)%20Orbitals.jpg) The
MCAS model will be used to inspect the bonding interactions of simple diatomic
molecules. The second period diatomic molecules use just the sp orbitals of the
currently accepted spdf model or the M/C orbitals of the MCAS model.
The
MCAS model will be used to inspect the bonding interactions of simple diatomic
molecules. The second period diatomic molecules use just the sp orbitals of the
currently accepted spdf model or the M/C orbitals of the MCAS model..jpg)
.jpg) The
figure at the right illustrates the situation with accompanying electrostatic
interactions. The electrostatic contours were determined with the nuclei at
their experimental distance apart and with the electrons at the orbital
extremes. Non-bonding electron charge was distributed uniformly to each lobe.
Classical electrostatic attractions and repulsions with were used. The
electrostatic images clearly demonstrate the surrounding symmetry of the
8-electron fluoride ion. They also demonstrate the weakness of the bond in the
fluorine molecule. There is little negativeness (blue in the figure) protecting
the molecule in this area. Consequently, fluorine is a very reactive
electron-acceptor. Thus, while “neighboring” atoms may join to lower their
individual vulnerabilities, this is inferior to having a full-time electron do
the job. The current practice of putting electrons between the nuclei at the
expense of de-shielding in other areas may be mathematically attractive, but it
is illogical from standard electrostatic interactions. That is why physics had
to be different at the atomic level. A bond represents electron-deficiency NOT
electron-abundance. Orbital overlap may, however, provide a conduit for
transient flow (!) of electrons from the antibonding quartet of one atom to
another.
The
figure at the right illustrates the situation with accompanying electrostatic
interactions. The electrostatic contours were determined with the nuclei at
their experimental distance apart and with the electrons at the orbital
extremes. Non-bonding electron charge was distributed uniformly to each lobe.
Classical electrostatic attractions and repulsions with were used. The
electrostatic images clearly demonstrate the surrounding symmetry of the
8-electron fluoride ion. They also demonstrate the weakness of the bond in the
fluorine molecule. There is little negativeness (blue in the figure) protecting
the molecule in this area. Consequently, fluorine is a very reactive
electron-acceptor. Thus, while “neighboring” atoms may join to lower their
individual vulnerabilities, this is inferior to having a full-time electron do
the job. The current practice of putting electrons between the nuclei at the
expense of de-shielding in other areas may be mathematically attractive, but it
is illogical from standard electrostatic interactions. That is why physics had
to be different at the atomic level. A bond represents electron-deficiency NOT
electron-abundance. Orbital overlap may, however, provide a conduit for
transient flow (!) of electrons from the antibonding quartet of one atom to
another..jpg) Consider
now the bonding in some simple diatom molecules as given by the MCAS model. The
figure at the right shows a plot of the experimental bond strength
Consider
now the bonding in some simple diatom molecules as given by the MCAS model. The
figure at the right shows a plot of the experimental bond strength.jpg) The
1st ionization potential of a single atom is now addressed. The
figure at the right shows the experimental data
The
1st ionization potential of a single atom is now addressed. The
figure at the right shows the experimental data.jpg) The
electron affinity of a single atom and its diatomic molecule is now addressed.
The figure at the right shows the experimental data
The
electron affinity of a single atom and its diatomic molecule is now addressed.
The figure at the right shows the experimental data.jpg) The
reason for the deviant electron affinities of the diatomic molecules becomes
clear when the electrostatic interactions are considered, especially the
enormously greater e-affinity of C-C. The figure at the right shows the
calculated positive and negative charge levels around the molecules in the MCAS
style with electrons at maximum orbital extension.
The
reason for the deviant electron affinities of the diatomic molecules becomes
clear when the electrostatic interactions are considered, especially the
enormously greater e-affinity of C-C. The figure at the right shows the
calculated positive and negative charge levels around the molecules in the MCAS
style with electrons at maximum orbital extension.
 Valence
bond theory would require 4 bonds between the carbon nuclei to give 8 shared
– this was never taught that I remember; but apparently is getting some press
Valence
bond theory would require 4 bonds between the carbon nuclei to give 8 shared
– this was never taught that I remember; but apparently is getting some press.jpg) Now
consider the carbon monoxide case. CO has the same number of electrons as does
nitrogen: 10. Unlike the case with nitrogen where each atom has the same number,
carbon has 4 and oxygen has 6. The figure at the right shows how the electrons
are redistributed when the CO molecule is formed. According to the MCAS
modeling, an electron from the “antibonding” orbital unit of oxygen is
transferred to the “bonding” orbital of carbon. This results in a permanent
dipole. With an electron arrangement like that of N2, CO should have
a bond strength attributed to a triple bond; actually it should be stronger
(experimentally observed) with the higher charge on oxygen tugging on the carbon
bonding electrons. I have included an MO description
Now
consider the carbon monoxide case. CO has the same number of electrons as does
nitrogen: 10. Unlike the case with nitrogen where each atom has the same number,
carbon has 4 and oxygen has 6. The figure at the right shows how the electrons
are redistributed when the CO molecule is formed. According to the MCAS
modeling, an electron from the “antibonding” orbital unit of oxygen is
transferred to the “bonding” orbital of carbon. This results in a permanent
dipole. With an electron arrangement like that of N2, CO should have
a bond strength attributed to a triple bond; actually it should be stronger
(experimentally observed) with the higher charge on oxygen tugging on the carbon
bonding electrons. I have included an MO description What
What k
with reciprocal motion for pairing. Clouds
connecting the
tops and bottoms of the p-orbitals are also envisioned
k
with reciprocal motion for pairing. Clouds
connecting the
tops and bottoms of the p-orbitals are also envisioned  The
figure at the right presents conceptual imagery of the Valence-Bond (VB),
Molecular Orbital (MO) and MCAS approaches to the hydrogen molecule. This allows
the three to be compared in the simplest molecular case.
The
figure at the right presents conceptual imagery of the Valence-Bond (VB),
Molecular Orbital (MO) and MCAS approaches to the hydrogen molecule. This allows
the three to be compared in the simplest molecular case.