Abstract
The current spdf-QM electron orbital model is a forced one based on the precepts of a spherical starting point that requires that macro-physical laws no longer apply. For atoms to actually bond to one another, atomic orbitals have to be “hybridized”.
π-bonds formed by overlapped, unhybridized, p-orbitals may make sense mathematically, assuming spin-reversal electron pairing actually occurs, but the nebulous clouds hardly make sense from a 3D, real world, perspective with mobile, interacting electrons. This paper looks at the sp-QM orbital hybridization from a 3D perspective, carries that hybridization a step further, and offers an alternative.
Introduction
The current spdf-QM electron orbital model of atoms is a forced one based on the precept of a spherical starting point. Not only does the QM model require established macro-physical laws to cease near the nucleus area, but the basic set of orbitals that are generated in the model have no resemblance to those needed to model the materials of our substantive world. For atoms to actually bond to one another, the spdf-QM orbitals have had to be “hybridized”. Initially, the hybridizing involved only the s and p-orbitals, but eventually essentially all of the orbitals had to be “hybridized” as metal complexes were modeled. This paper looks at the “hybridizing” of the s and p-orbitals. It should be noted that, despite the extensive “hybridizing” of all the other atomic orbitals, the spherical 1s-orbitals of hydrogen and helium have been off limits. [A non-spherical starting point addresses hydrogen’s position in the period table[1]; hydrogen’s bonding with itself[2] and its bonding between two oxygen atoms[3] and between two boron atoms[4]; and helium’s ortho/para phenomenon[5].]
Before addressing the mechanics of “atomic orbital hybridization and atom bonding”, it is appropriate to note that experimental data [6] demonstrates that electrons are observed as particles and do not exist everywhere at once [7] . Orbitals should be considered as defining where electrons occur around a nucleus and where atom-atom interactions can occur. A ‘hard’ orbital gives a sense of behavioral constancy and 3-dimensional direction of electron movement or static presence. It is this 3-D modeling that practitioners find useful in assembling atoms like tinker-toys into molecules.
While physicists were content with the “file-cabinet stacking” of spdf orbitals for their spectral data, chemists were unable to explain the geometry of real molecules with them. As G.N Lewis was pointing out in the early 1900s, simple real molecules followed a “rule-of-eight”. Thus, methane (CH4) had its 4 hydrogen atoms in a tetrahedral arrangement around a carbon center. The orthogonal projection of the p-orbitals and the spherical s-orbital did not yield the correct structure even for this simplest of molecules. The octet rule imagery, on the other hand, gave good indications of molecular form. Elementary level, “tinker toy”, ball-and-stick models still provide the best simple, “hands-on”, understanding of atomic interactions, in my estimation, with a caveat about just what those stick single and spring “double and triple” bonds actually are. The equivalent 2-D paper representations are also quite useful to the chemist who is interested, for example, in replacing “the multiple bond” between two atoms with bonds to each of them by two other atoms.
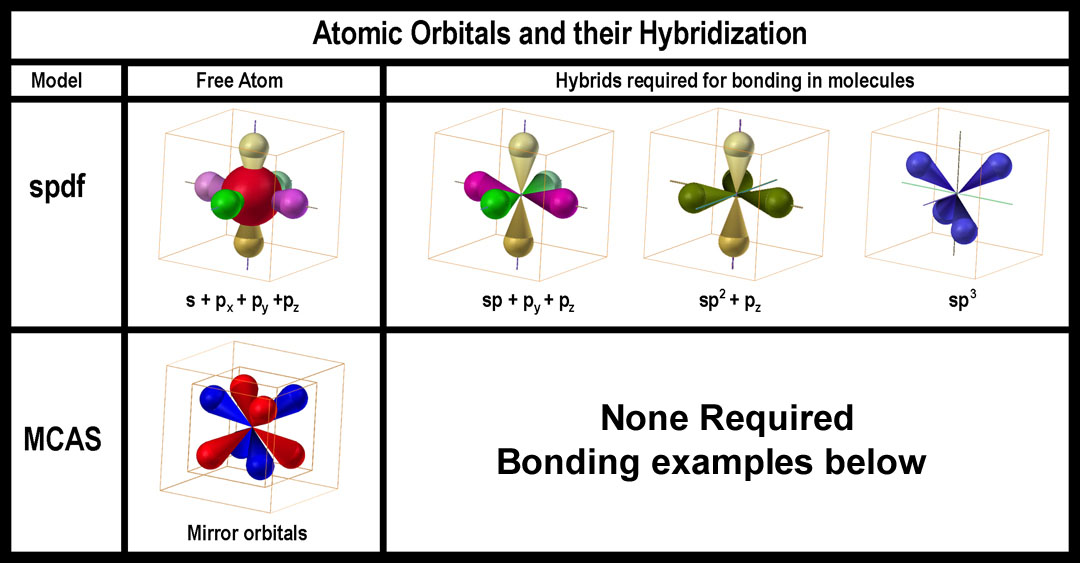
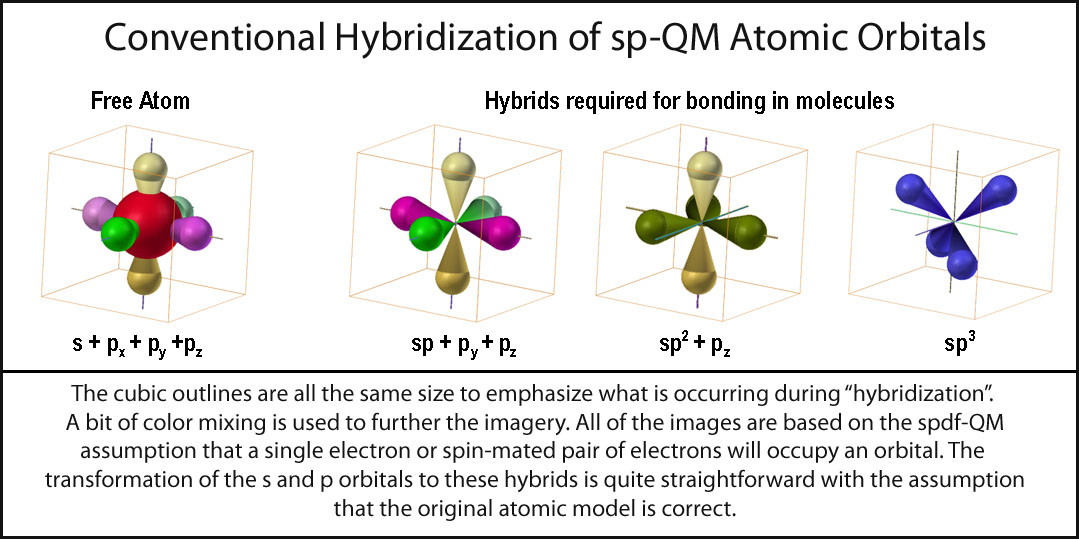 In the early efforts of molecular modeling, it was accepted that the spdf-QM model was correct for individual atoms. If molecules needed different ones, then so be it. The logical approach was to determine what orbitals “were needed” for real molecules and to “hybridize” (mix, whirl, blend, whatever) the atomic ones to give these “needed” ones. The simplest cases to be addressed by “atomic orbital hybridization” were linear, trigonal, and tetrahedral arrangements of atoms. To this end, the s and p orbitals were combined in three ways: s+1p (sp), s+2p’s (sp2), and s+3p’s (sp3). In the current spdf-hybridization, the s-orbital combines with the p-orbitals to produce a major plus (+) lobe and a tiny negative (-) lobe. Presumably as an orbital, the s-orbital is synchronous +/-! [As noted above, an s-orbital is not “hybridized” to complimentary tetrahedral orbitals (t+ and t-).] Thus, a s-orbital combining with a p-orbital should have 4 equal lobes (2+ and 2-). Eight (8) lobes are maintained in the various hybrids. In the sp1-hybrid, the “negative lobes” coincide with the positive lobes in linear fashion and are ignored. For the sp2 and sp3 hybrids, the complementary lobes are also simply ignored or shown as tiny insignificant appendages. The sp, sp2, and sp3 hybrid sets are shown in the figure on the right.
In the early efforts of molecular modeling, it was accepted that the spdf-QM model was correct for individual atoms. If molecules needed different ones, then so be it. The logical approach was to determine what orbitals “were needed” for real molecules and to “hybridize” (mix, whirl, blend, whatever) the atomic ones to give these “needed” ones. The simplest cases to be addressed by “atomic orbital hybridization” were linear, trigonal, and tetrahedral arrangements of atoms. To this end, the s and p orbitals were combined in three ways: s+1p (sp), s+2p’s (sp2), and s+3p’s (sp3). In the current spdf-hybridization, the s-orbital combines with the p-orbitals to produce a major plus (+) lobe and a tiny negative (-) lobe. Presumably as an orbital, the s-orbital is synchronous +/-! [As noted above, an s-orbital is not “hybridized” to complimentary tetrahedral orbitals (t+ and t-).] Thus, a s-orbital combining with a p-orbital should have 4 equal lobes (2+ and 2-). Eight (8) lobes are maintained in the various hybrids. In the sp1-hybrid, the “negative lobes” coincide with the positive lobes in linear fashion and are ignored. For the sp2 and sp3 hybrids, the complementary lobes are also simply ignored or shown as tiny insignificant appendages. The sp, sp2, and sp3 hybrid sets are shown in the figure on the right.
Parsing the sp-QM Hybridization and Bonding Concept
In current methodology, “molecular orbitals” are formed from overlapped hybrid atomic orbitals that have the same electron occupancy assumptions as the hybrid atomic orbitals do. An in-axis molecular orbital is straightforward for each of the atomic hybrids assuming that the vernacular of the QM mated-pair of electrons is correct. It is a bit of a problem accepting that a pair of electrons just mill around in the confined space between the nuclei, however. One of the attributes of mathematical treatments of bonding (and the focus of the MO approach, for that matter) is that one does not actually need to know how things work, only that they do.[8]
 Maximum bonding should occur when the orbitals of two atoms from a linear molecular orbital (bond) between the two atoms. While it is traditional to present sp3–sp3 bonding first, sp2-sp2 bonding is discussed here first. The figure at the right allows in-axis (on a line from nucleus to nucleus) and off-axis interactions to be seen.
Maximum bonding should occur when the orbitals of two atoms from a linear molecular orbital (bond) between the two atoms. While it is traditional to present sp3–sp3 bonding first, sp2-sp2 bonding is discussed here first. The figure at the right allows in-axis (on a line from nucleus to nucleus) and off-axis interactions to be seen.
The in-axis orbital overlap [called a sigma (σ) bond] indicated in the first image is easily grasped. It is the orbital occupancy of spin-paired electrons that is more difficult.
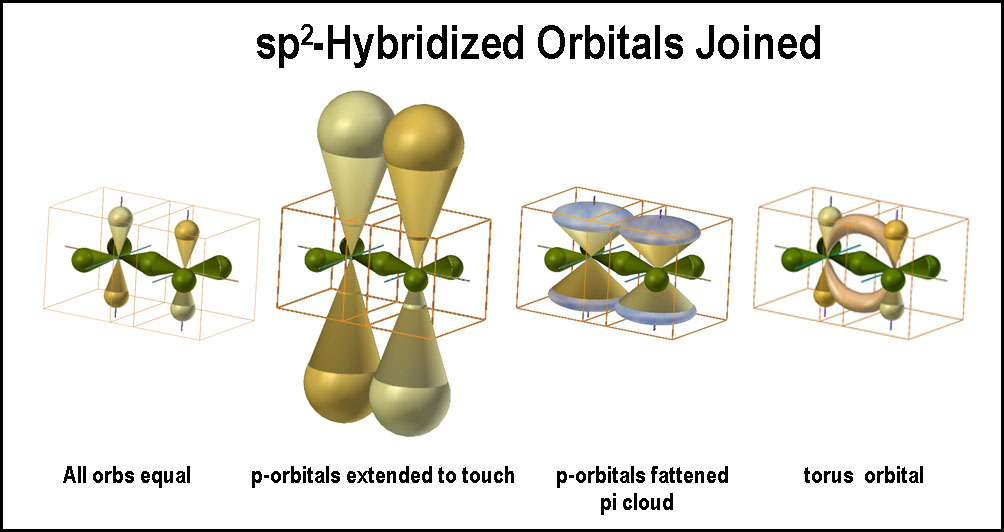
Overlap of the p-orbitals is more difficult to comprehend as they are parallel to one another. Convention teaches that these adjacent, parallel, “unhybridized”, p-orbitals form a strong π-bond. Taught and accepted; believable and correct? The second image in the figure shows greatly extended p-orbitals to effect “touching” and the extreme bending angle of the bond. The third image shows flattened p-orbitals with the touching portions forming “π-clouds”. Just how these “clouds” of electrons hold the nuclei together is a bit dicey.
According to the spdf-QM model an electron has an equal probability of being in each lobe of an orbital (hybridized or not); how they do that is another matter. In other words, particulate electrons “flow” through the lobes of an orbital “freely” to populate them equally. With this in mind, the atoms are shown linked as a torus in the fourth image of the joined “sp2 hybridized orbitals”. (The p-orbitals are left to indicate what needs to happen.) Obviously there needs to be much bending of the p-orbitals to accomplish this. What this indicates is that the bond is NOT between two parallel “8”-shaped orbitals, but rather between two “<”-shaped orbitals, or, more likely, one side of an X-shaped orbital. What is a bent p-orbital, but a “self-hybrid” orbital? More later.
The interaction of two atoms with three different degrees of spx-hybridization is shown in the next figure without considering electron loading or other atoms attached.
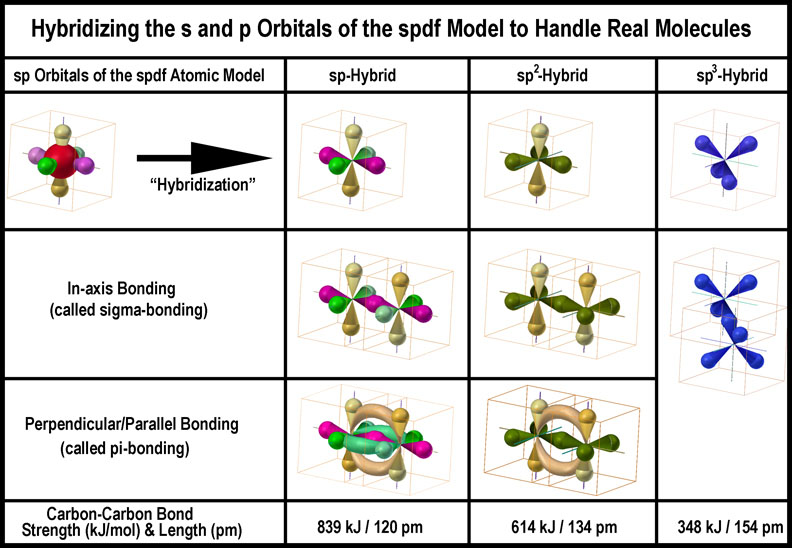
Bent bonds are energetically higher in energy and thus less stable. That highly “bent bonds” can provide the large incremental bonding strengths[9] indicated in the bottom of the above figure seems improbable.
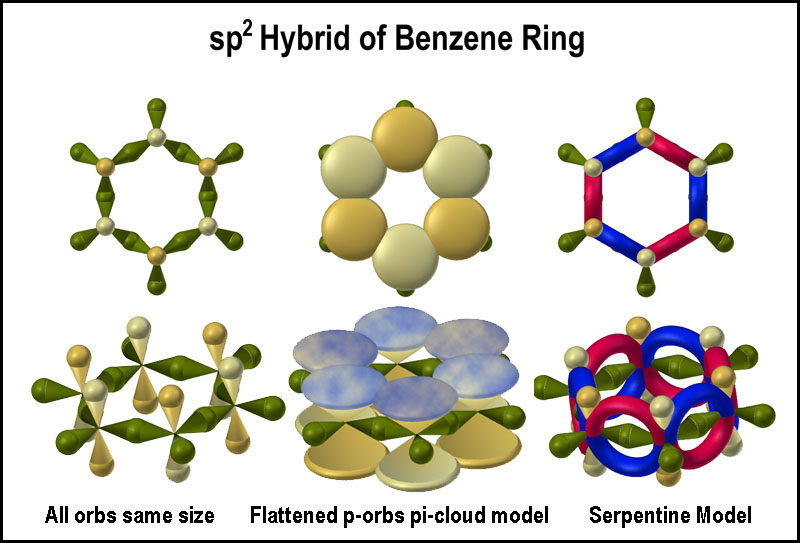
The “π-cloud” alluded to for p-p orbital bonding is a key feature in describing benzene and other aromatic compounds. The σ-bond network is shown in the left images of the figure on the right. The flattened p-orbitals and π-cloud are shown in the next images. While the p-orbital overlap issue was pointed out for a simple double bond, the interlaced π-cloud presents a number of other issues: how do particulate electrons flows round an atom, between atoms and through the “cloud”? The traffic flow issue is easily handled by mirrored serpentine orbitals as seen in the last image in the figure. This provides electron density above and below the 6-carbon plane. The above and below plane atomic orbitals of the serpentine molecular orbitals are clearly not vertical "8"-shaped ones, but rather crossed orbitals; in other words, they form an X. While 3D orbital models provide pleasant imagery, many chemists find simple Kekulé-type images[10] provide an easier understanding of how and why olefins and aromatic compounds behave the way they do chemically.[11]
Carrying Orbital Hybridization a Step Further
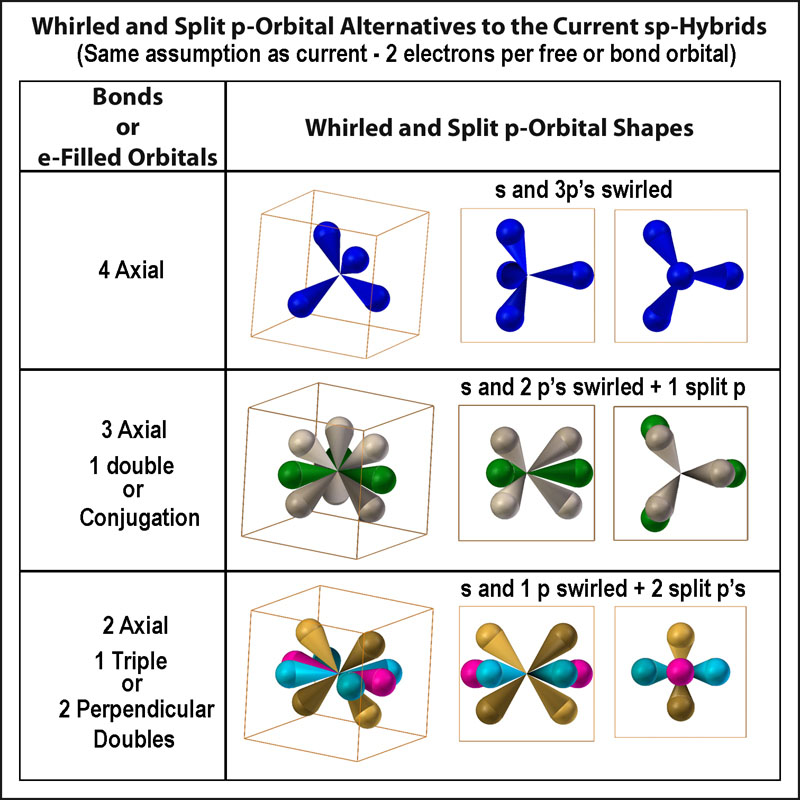 Pre-computer mathematical modeling was mostly xyz-coordinate driven. The first emphasis was on linear, then planar, and finally 3-D.With the need fordirectionally oriented orbitals, the simplest hybridizing of the orbitals evolved. The tetrahedral sp3 could handle many connection issues and even some non-tetrahedral ones like ethylene, allene, carbon dioxide. Planar, non-linear connections, like those needed for carbonate ions and aromatic molecules were the problem. So, p’s were whirled with the s. Why stop with whirled p’s? Why not “split p’s”? If entirely different atomic orbital sets can be chosen (and, yes, there are several!)[12] and orbitals can be merged and split into differing sets, then it hardly seems a problem to just split an orbital without merging it. The figure at the right shows “whirled and split p-orbital” alternatives to the current sp, sp2, and sp3 hybrids. These alternatives provide significant orbital overlap where perpendicular p’s do not.
Pre-computer mathematical modeling was mostly xyz-coordinate driven. The first emphasis was on linear, then planar, and finally 3-D.With the need fordirectionally oriented orbitals, the simplest hybridizing of the orbitals evolved. The tetrahedral sp3 could handle many connection issues and even some non-tetrahedral ones like ethylene, allene, carbon dioxide. Planar, non-linear connections, like those needed for carbonate ions and aromatic molecules were the problem. So, p’s were whirled with the s. Why stop with whirled p’s? Why not “split p’s”? If entirely different atomic orbital sets can be chosen (and, yes, there are several!)[12] and orbitals can be merged and split into differing sets, then it hardly seems a problem to just split an orbital without merging it. The figure at the right shows “whirled and split p-orbital” alternatives to the current sp, sp2, and sp3 hybrids. These alternatives provide significant orbital overlap where perpendicular p’s do not.
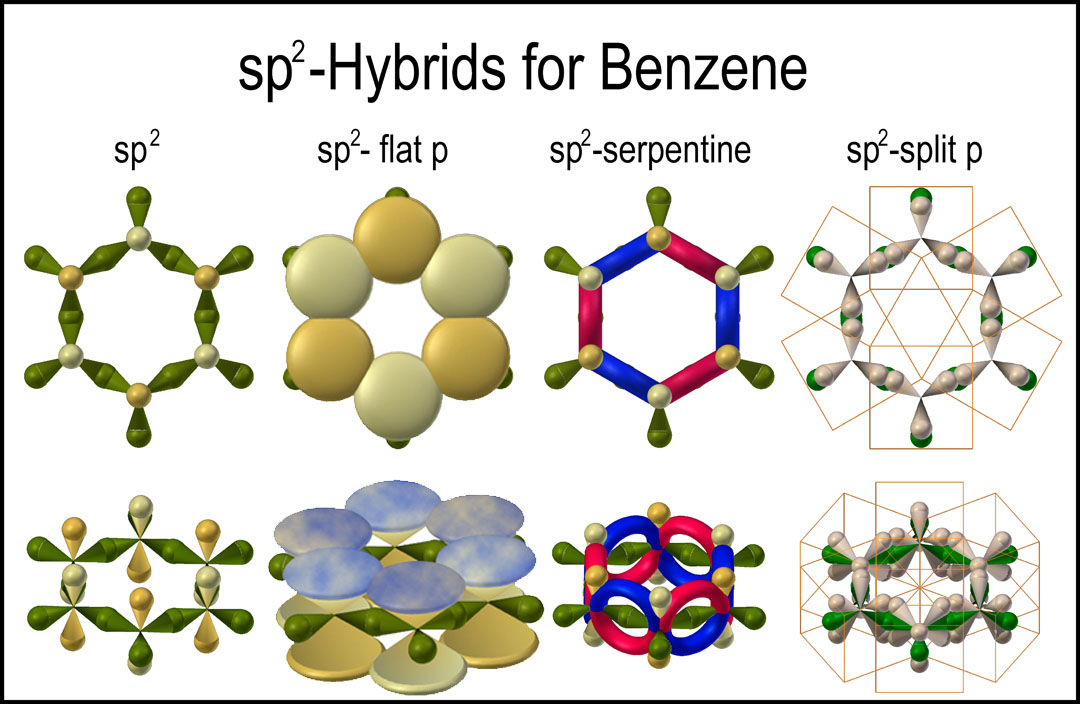 The benzene carbon network modeled with the sp2-split-p orbital hybrid is now added to the other models in the figure on the right. The π-bonds are not fully overlapped here in order not to conceal the σ-bonds below. The sigma bond is now surrounded by two orbital lobes with time averaged <1 electron. Compare this with a sp3 sigma bond where its end of the bond would have three orbitals with an electron each. The p-NMR response of attached hydrogen atoms would be different because of the difference in shielding and, indeed, such is observed.
The benzene carbon network modeled with the sp2-split-p orbital hybrid is now added to the other models in the figure on the right. The π-bonds are not fully overlapped here in order not to conceal the σ-bonds below. The sigma bond is now surrounded by two orbital lobes with time averaged <1 electron. Compare this with a sp3 sigma bond where its end of the bond would have three orbitals with an electron each. The p-NMR response of attached hydrogen atoms would be different because of the difference in shielding and, indeed, such is observed.
Consider now the carbonate anion. sp2 hybrid models, resonance forms, a MO diagram of the π-system, and a sp2-split-p model are shown in the figure below.
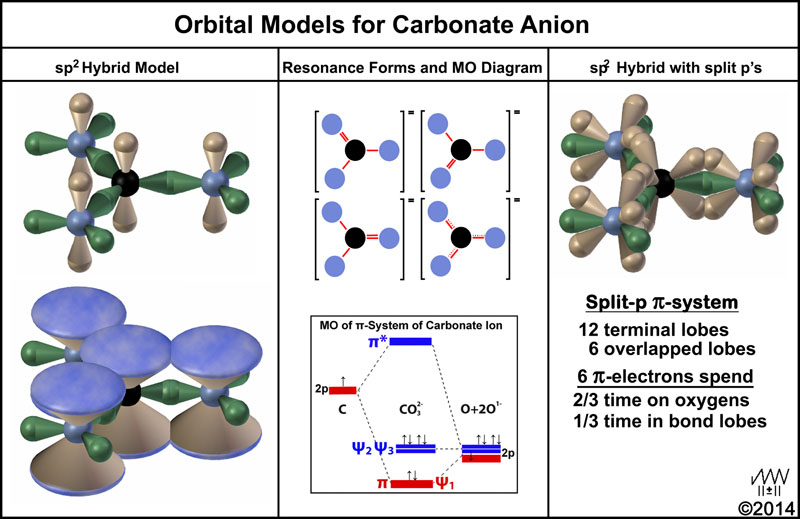
The upper left image is the typical sp2-p model without p-p bridging. The lower left shows the π-in-the-sky cloud representation. How the 6-electrons of the p-orbitals move around in this cloud is very vague. The upper middle images show the venerable resonance forms that indicate that these 6-electrons move back-and-forth from carbon to oxygen. Actually, there should be a fourth form shown in which there is no π-bond (net positive carbon and three negative oxygen atoms). The dotted line form is intended to summarize the three other forms. The MO image[13] in the lower middle conveys what one of the three “double-bond resonance forms” indicates. This is used to indicate that the C-O bonds are 1/3rd order with respect of the π-bonds. Of course, one would expect all 6-electrons to be equal. So three of these MO forms would be needed, too.
The image on the right of the figure illustrates the situation when the p-orbitals are split-p’s. Electrons are assumed to flow from atom to atom through the connected orbital lobes. Click here for a shockwave file by the author of a particle moving in an elliptical orbit. As indicated in the figure, each electron will spend 1/3rd of its time in the overlapped orbital lobes (bonds) and 2/3rd of its time in the terminal lobes of the oxygen atoms. Since there are 6-electrons, 2 will, on average, be in overlapped orbitals at any given time. Since the electrons are “paired” they must be so by reciprocal motion; a tenet of the MCAS model.
Of course, the question is whether an atom “hybridizes”. The answer is that the spdf-QM model leaves no other choice. By requiring electrons to be spin-paired, the model restricted the number of orbitals to half the number of total possible orbitals. This, in turn, greatly restricted the number of bonding options.
Consider a Different Approach
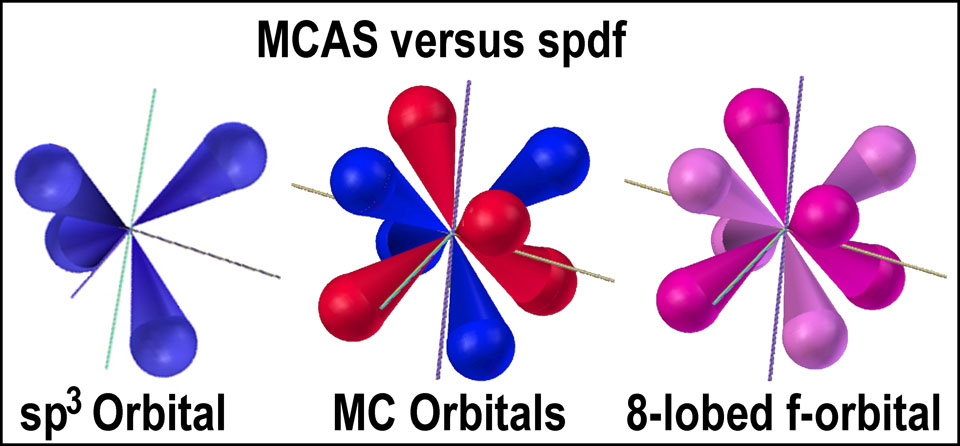 Consider the MCAS atomic model which does not require ‘hybridization” as it is already in the needed form. The MCAS model also has the needed “mirrored” orbitals that negate the need for spin-reversed pairing of electrons in the same orbital and provides the mechanism for electron flow in aromatic compounds. It also provides twice the number of orbitals that can be used for bonding; thus, it provides options not possible with the spx-hybrids.
Consider the MCAS atomic model which does not require ‘hybridization” as it is already in the needed form. The MCAS model also has the needed “mirrored” orbitals that negate the need for spin-reversed pairing of electrons in the same orbital and provides the mechanism for electron flow in aromatic compounds. It also provides twice the number of orbitals that can be used for bonding; thus, it provides options not possible with the spx-hybrids.
Note the similarity of the sp3-QM orbital and a MC orbital of the MCAS model. spdf-QM has provided the precedence for the MC orbitals in its 8-lobed f-orbital. The difference is that the two 4-lobed, tetrahedral MC orbitals are separate with an electron able to move within a tetrahedral group. Up to 4 electrons can be accommodated as the tetrahedral unit has 4-lobes. The f-orbital has a +/- tetrahedral pair also, but only one or two electrons are deemed able to occupy ALL of the lobes equally. How they do so is not clear. Unlike the MC orbitals, the 8-lobed f-orbital is not allowed to contain more than 2 electrons and those two are said to be spin-paired.
The MC orbitals provide a simpler set of orbitals compared to those of the hybridized sp-QM orbitals. There is no need to have two electrons occupy the same orbital via spin-reversal of an electron. There is also no need for hybridization of the MC orbitals and certainly not for simple molecules! Two summary figures are presented below.
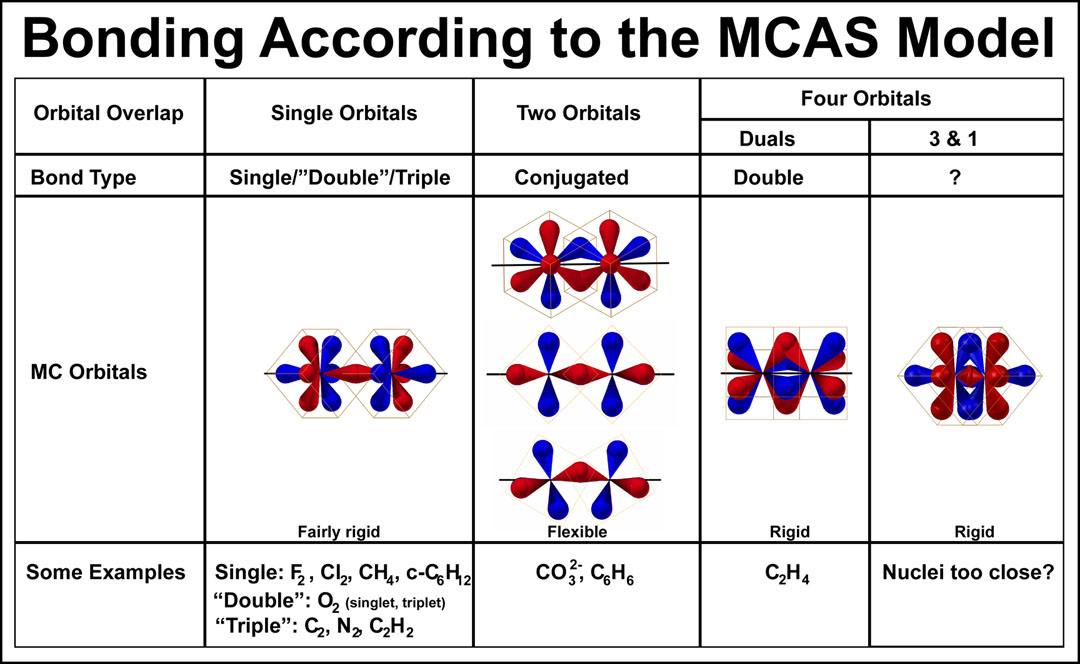
The ways in which the mirrored tetrahedral pairs can overlap between two atoms is easily comprehended. It is their electron-filling and connection to other atoms that requires more attention. The internuclear distance of the overlap modes decreases from left to right in the figure below. Briefly, the “single”, “two”, and “four” overlapped orbitals relate to the single, conjugated, and isolate double bonds that are typically taught.
.jpg) As indicated in “Some Examples”, the single orbital overlap can cover more than common single bonds. Indeed, the diatomic molecules of the second row of the periodic table are properly described by the single orbital overlap model — the strengths of the bonds (single, double, triple) are just related to the amount of anti-bonding electrons (those in blue orbitals in the figure on the right; those orbitals, incidentally, are part of the tetrahedral orbital unit that forms the overlap bond!). The singlet/triplet oxygen duality is caused by different distributions of the electrons in the bonding and antibonding orbitals. A discussion of these phenomena can be found in Understanding the Bonding of Second Period Diatomic Molecules[14] . The image is hyperlinked to the article.
As indicated in “Some Examples”, the single orbital overlap can cover more than common single bonds. Indeed, the diatomic molecules of the second row of the periodic table are properly described by the single orbital overlap model — the strengths of the bonds (single, double, triple) are just related to the amount of anti-bonding electrons (those in blue orbitals in the figure on the right; those orbitals, incidentally, are part of the tetrahedral orbital unit that forms the overlap bond!). The singlet/triplet oxygen duality is caused by different distributions of the electrons in the bonding and antibonding orbitals. A discussion of these phenomena can be found in Understanding the Bonding of Second Period Diatomic Molecules[14] . The image is hyperlinked to the article.
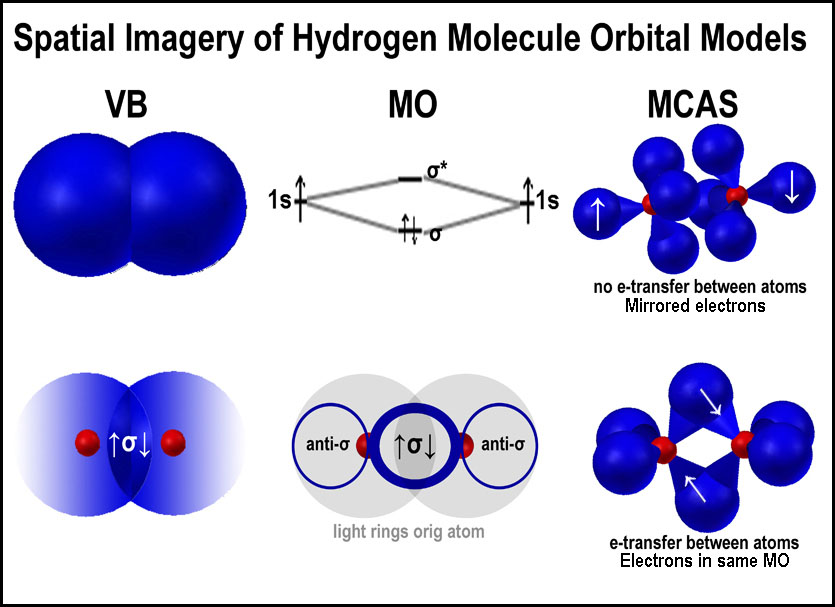 Application of the MCAS model to the hydrogen molecule can be found in Comparing Several Orbital Approaches to the Hydrogen Molecule.2 The image on the right is hyperlinked to the article. Only one of the tetrahedral orbital units of each hydrogen atom is shown in the figure.
Application of the MCAS model to the hydrogen molecule can be found in Comparing Several Orbital Approaches to the Hydrogen Molecule.2 The image on the right is hyperlinked to the article. Only one of the tetrahedral orbital units of each hydrogen atom is shown in the figure.
Several more examples are now presented for the MCAS approach.

The carbon structure of cyclohexane in its chair conformation is shown on the right. The four electrons of each carbon are unshared and in the blue orbitals. Bonding between carbon atoms and to other atoms, such as hydrogen, is through the red orbitals. Electrons in the three blue orbitals surrounding each bond provide the electrostatic attraction with the nucleus on the other end of the bond that gives the bond its strength. 60° staggering and eclipsing energies are related to the electrostatic interactions of the 6 blue orbitals around a bond as rotation around the bond occurs. Rotation about a C―C bond is limited to flexing in cyclohexane, but occurs "freely" in molecules like ethane and butane.
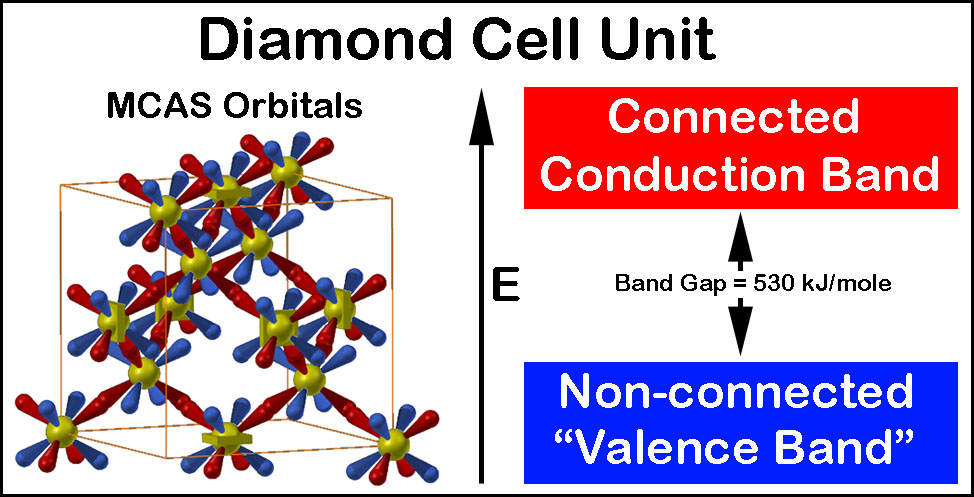 The reader might find it interesting that crystalline carbon is simply repetitive C6 carbon chair units in 3D.[15]
The reader might find it interesting that crystalline carbon is simply repetitive C6 carbon chair units in 3D.[15]
The crystal bond network (red in the figure on the right that is hyperlinked to the article) of pure carbon has no electrons in it. This is the conduction band! The band gap is the energy required to move an electron from an atom's "non-sharing", tetrahedral orbital unit to its overlapped orbital, sharing network. Extremely tiny amounts (<1 per 10,000 cell units!) of interstice-doping with electron or hole providing atoms allows it and silicon to be semiconductors.
-
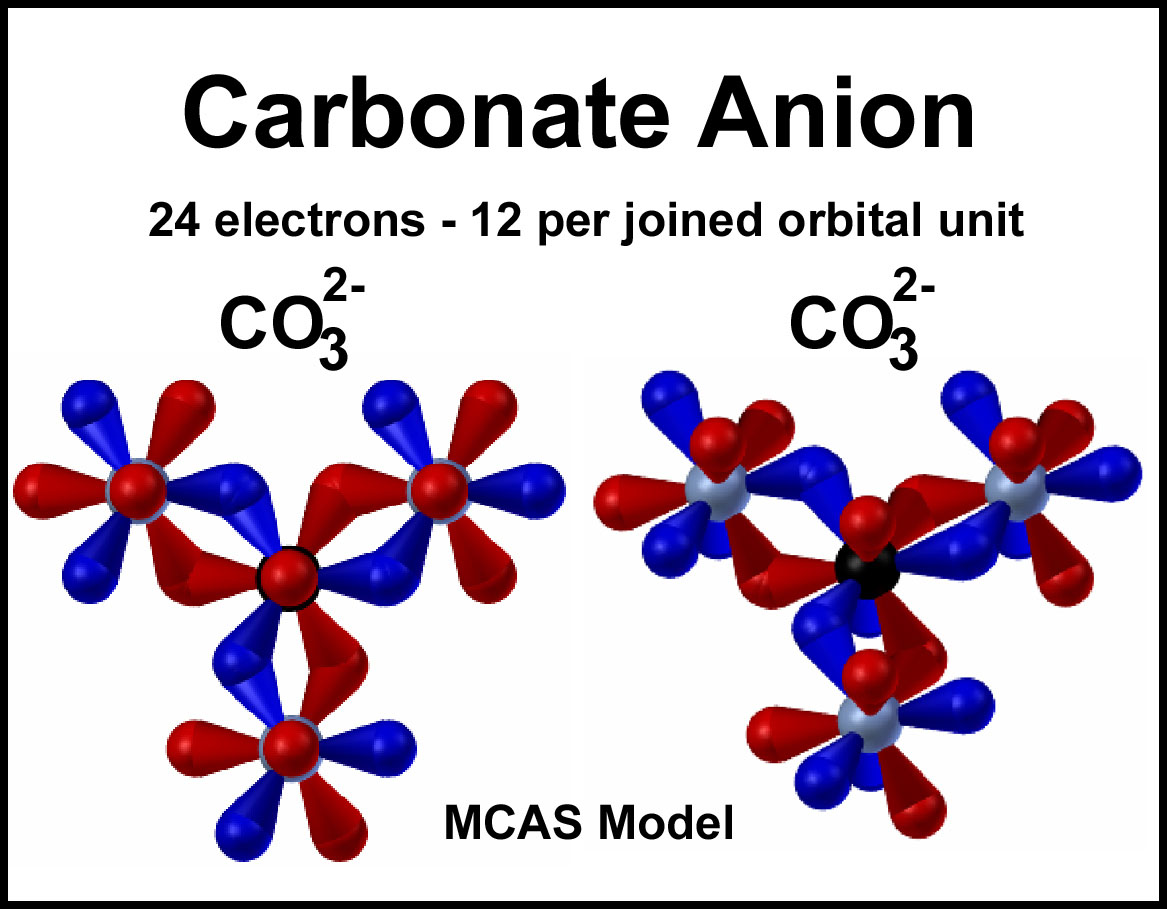 The MCAS orbital structure for the carbonate anion is shown on the right. Note the reciprocal configuration of the red and blue orbital units. There are 26 orbitals (6 bonds and 20 terminals). Start with 6 electrons in each of the oxygen terminal orbitals and 6 in the overlapped orbitals; this is the fourth resonance form described above where there is a net -1 around each of the oxygen atoms and a net +1 around the central carbon atom (assigning half a bond electron to each of the atoms that forms the bond. Electrons flow through each joined orbital unit (red and blue) reciprocally to give the average of all the other resonance forms and to provide "pairing".
The MCAS orbital structure for the carbonate anion is shown on the right. Note the reciprocal configuration of the red and blue orbital units. There are 26 orbitals (6 bonds and 20 terminals). Start with 6 electrons in each of the oxygen terminal orbitals and 6 in the overlapped orbitals; this is the fourth resonance form described above where there is a net -1 around each of the oxygen atoms and a net +1 around the central carbon atom (assigning half a bond electron to each of the atoms that forms the bond. Electrons flow through each joined orbital unit (red and blue) reciprocally to give the average of all the other resonance forms and to provide "pairing".
As noted in the beginning, the MCAS model starts with a different base orbital: a tetrahedral one instead of a spherical one. In doing so, it handles many of the current ambiguous orbital issues, such as hydrogen’s position in the period table, hydrogen’s bonding with itself, and its bonding between two oxygen atoms and between two boron atoms, and helium’s ortho/para phenomenon, without the need to “hybridize”!
REFERENCES
[6] A. S. Stodolna1, A. Rouzée, F. Lépine, S. Cohen, F. Robicheaux, A. Gijsbertsen, J. H. Jungmann, C. Bordas, and M. J. J. Vrakking, Hydrogen Atoms under Magnification: Direct Observation of the Nodal Structure of Stark States, Phys. Rev. Lett. 110, 213001 (2013)


 In the early efforts of molecular modeling, it was accepted that the spdf-QM model was correct for individual atoms. If molecules needed different ones, then so be it. The logical approach was to determine what orbitals “were needed” for real molecules and to “hybridize” (mix, whirl, blend, whatever) the atomic ones to give these “needed” ones. The simplest cases to be addressed by “atomic orbital hybridization” were linear, trigonal, and tetrahedral arrangements of atoms. To this end, the s and p orbitals were combined in three ways: s+1p (sp), s+2p’s (sp2), and s+3p’s (sp3). In the current spdf-hybridization, the s-orbital combines with the p-orbitals to produce a major plus (+) lobe and a tiny negative (-) lobe. Presumably as an orbital, the s-orbital is synchronous +/-! [As noted above, an s-orbital is not “hybridized” to complimentary tetrahedral orbitals (t+ and t-).] Thus, a s-orbital combining with a p-orbital should have 4 equal lobes (2+ and 2-). Eight (8) lobes are maintained in the various hybrids. In the sp1-hybrid, the “negative lobes” coincide with the positive lobes in linear fashion and are ignored. For the sp2 and sp3 hybrids, the complementary lobes are also simply ignored or shown as tiny insignificant appendages. The sp, sp2, and sp3 hybrid sets are shown in the figure on the right.
In the early efforts of molecular modeling, it was accepted that the spdf-QM model was correct for individual atoms. If molecules needed different ones, then so be it. The logical approach was to determine what orbitals “were needed” for real molecules and to “hybridize” (mix, whirl, blend, whatever) the atomic ones to give these “needed” ones. The simplest cases to be addressed by “atomic orbital hybridization” were linear, trigonal, and tetrahedral arrangements of atoms. To this end, the s and p orbitals were combined in three ways: s+1p (sp), s+2p’s (sp2), and s+3p’s (sp3). In the current spdf-hybridization, the s-orbital combines with the p-orbitals to produce a major plus (+) lobe and a tiny negative (-) lobe. Presumably as an orbital, the s-orbital is synchronous +/-! [As noted above, an s-orbital is not “hybridized” to complimentary tetrahedral orbitals (t+ and t-).] Thus, a s-orbital combining with a p-orbital should have 4 equal lobes (2+ and 2-). Eight (8) lobes are maintained in the various hybrids. In the sp1-hybrid, the “negative lobes” coincide with the positive lobes in linear fashion and are ignored. For the sp2 and sp3 hybrids, the complementary lobes are also simply ignored or shown as tiny insignificant appendages. The sp, sp2, and sp3 hybrid sets are shown in the figure on the right.








.jpg)



 The MCAS orbital structure for the carbonate anion is shown on the right. Note the reciprocal configuration of the red and blue orbital units. There are 26 orbitals (6 bonds and 20 terminals). Start with 6 electrons in each of the oxygen terminal orbitals and 6 in the overlapped orbitals; this is the fourth resonance form described above where there is a net -1 around each of the oxygen atoms and a net +1 around the central carbon atom (assigning half a bond electron to each of the atoms that forms the bond. Electrons flow through each joined orbital unit (red and blue) reciprocally to give the average of all the other resonance forms and to provide "pairing".
The MCAS orbital structure for the carbonate anion is shown on the right. Note the reciprocal configuration of the red and blue orbital units. There are 26 orbitals (6 bonds and 20 terminals). Start with 6 electrons in each of the oxygen terminal orbitals and 6 in the overlapped orbitals; this is the fourth resonance form described above where there is a net -1 around each of the oxygen atoms and a net +1 around the central carbon atom (assigning half a bond electron to each of the atoms that forms the bond. Electrons flow through each joined orbital unit (red and blue) reciprocally to give the average of all the other resonance forms and to provide "pairing".